Computational Intelligence for Integrated Design
-
Intro
-
WS 1: Probability & Statistics
-
WS2: Optimization
-
WS 3: Supervised Learning I
-
WS 4: Supervised Learning II
-
WS 5: Unsupervised Learning
-
WS 6: Reinforcement Learning
-
Supplemental Materials
-
Past Course Projects
Information
| Course Code | AR0202 |
| Last updated | April 23, 2025 |
| Keywords | |
| Primary study | Master |
| Secondary study | BK Master |
Responsible
| Teachers | |
| Faculty |
Computational Intelligence for Integrated Design 0/8
Computational Intelligence for Integrated Design
In this course, you learn about Computational Intelligence for integrated approaches bridging Architectural Design and Engineering.
Course Overview
Computational Intelligence encompasses theory and application of computational methods, techniques and tools that have the ability to learn based on given datasets, models and tasks. It includes AI comprising machine learning, bringing together concepts from probability and statistics to programming and optimisation. It is increasingly applied in the building sector, both to help understand the current status of built environment and to make informed (design) decisions based on predicted future responses. It mines data and translates them into actionable information. It harnesses and helps understanding information to turn it into applicable knowledge. This course focuses on Computational Intelligence for Integral Design in architecture and engineering, intended as a process of integration across disciplines.
In this course, you will learn Computational Intelligence techniques and apply them in Architectural Design and Engineering. To learn the techniques, this online material provides you tutorials and examples. Topics of optimisation, probabilistic analysis, and machine learning will be covered, from distribution fitting and sampling, to regression, neural networks, and evolutionary algorithms, among others.
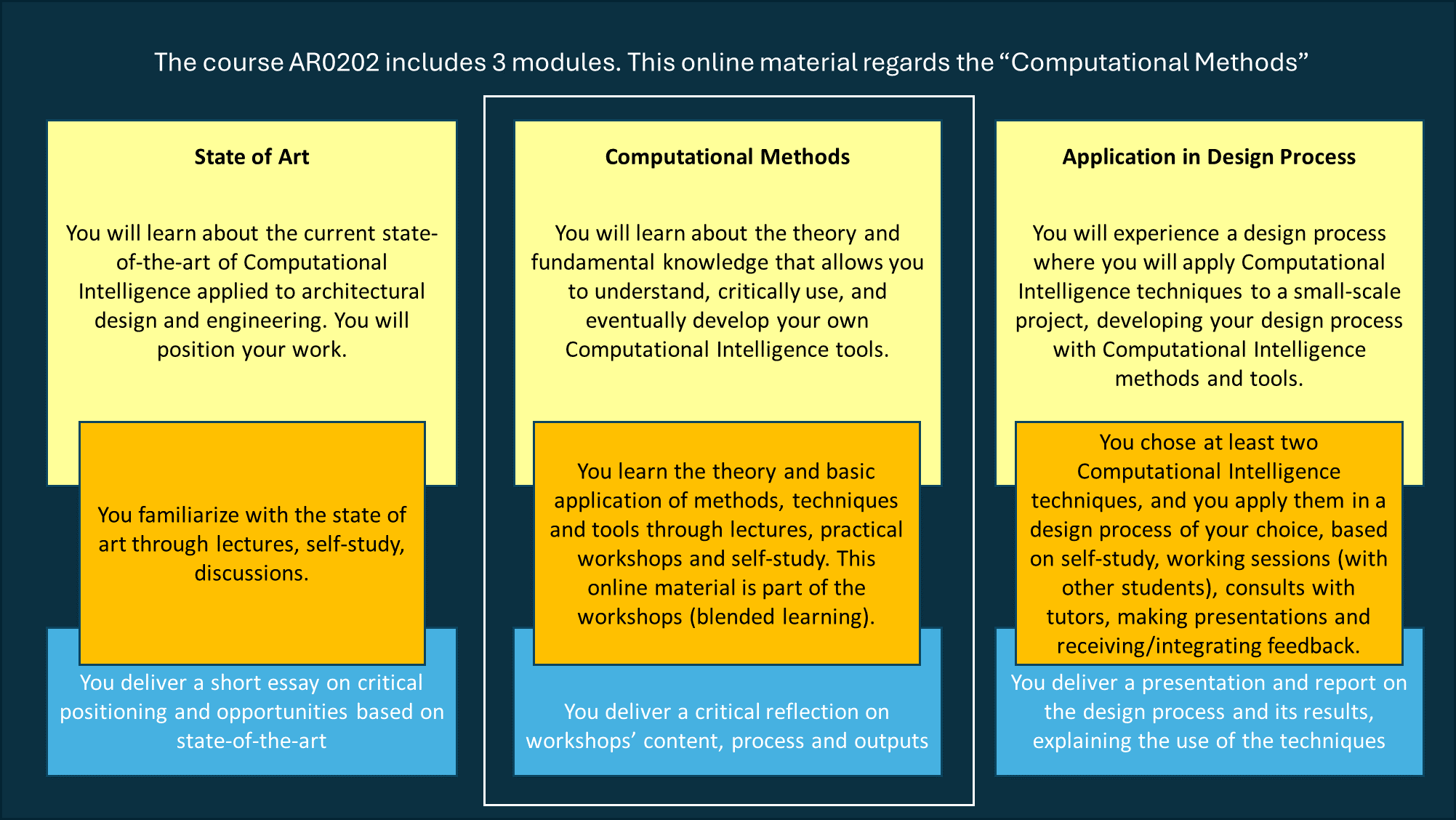
This online material is part of a MSc course at TU Delft. If you are attending the TU Delft MSc course, you will learn about the current state-of-the-art of Computational Intelligence applied to architectural design and engineering, and about the theory and fundamental knowledge required to understand how to critically use (and eventually develop) your own Computational Intelligence tools. You will also experience a design process where you will apply such techniques to a small-scale project, developing your design process with Computational Intelligence methods and tools. In class you will be assisted with exercises, attend lectures and discussions on the state-of-the-art in academia and practice, and tutored on the design assignment of your choice. You can see examples of projects completed in past years under the Past Course Projects chapter.
Study Materials
A basic level of Python is helpful to have at the start of the course. We recommend reviewing the following materials:
Python Programming and Numerical Methods: A Guide for Engineers and Scientists (first 4 chapters)
Additional Literature
- Wortmann, T., 2018. Efficient, Visual, and Interactive Architectural Design Optimization with Model-based Methods
- Wortmann, T., Cichocka, J. and Waibel, C., 2022. Simulation-based Optimization in Architecture and Building Engineering – Results from an International User Survey in Practice and Research. Energy and Buildings, p.111863.
- Ekici, B., Turkcan, O.F., Turrin, M., Sariyildiz, I.S. and Tasgetiren, M.F., 2022. Optimising High-Rise Buildings for Self-Sufficiency in Energy Consumption and Food Production Using Artificial Intelligence: Case of Europoint Complex in Rotterdam. Energies, 15(2), p.660.
- Pan, W., Sun, Y., Turrin, M., Louter, C. and Sariyildiz, S., 2020. Design exploration of quantitative performance and geometry typology for indoor arena based on self-organizing map and multi-layered perceptron neural network. Automation in Construction, 114, p.103163.
- Andriotis, C., 2019. Data driven decision making under uncertainty for intelligent life-cycle control of the built environment.
Computational Intelligence for Integrated Design 1/8
WS 1: Probability & Statisticslink copied
Probability and statistics are fundamental to the field of machine learning and artificial intelligence (AI). Probability provides a mathematical framework to model uncertainty, enabling predictions and inferences based on data. Statistics, on the other hand, involves the collection, analysis, and interpretation of data, providing tools to make sense of and extract meaningful patterns from complex datasets. Together, these disciplines form the backbone of many machine learning algorithms, allowing AI systems to learn from data, make decisions under uncertainty, and improve over time through experience. Whether it’s in classification, regression, or clustering tasks, probability and statistics are essential in designing and understanding the behavior of AI models.
Estimation & Sampling
Estimation and sampling techniques are crucial in machine learning, enabling models to make predictions and generalize from limited data. Estimation refers to the process of inferring the values of unknown parameters in a model based on observed data. Common methods include Maximum Likelihood Estimation (MLE) and Bayesian estimation, both of which help in determining the most probable parameters that explain the data. Sampling techniques, such as random sampling, bootstrapping, and Monte Carlo methods, allow models to approximate distributions and perform tasks like parameter estimation or uncertainty quantification. In machine learning, these techniques are vital for training models on large datasets, improving model accuracy, and ensuring that the models can generalize well to unseen data by effectively capturing the underlying data distribution.
Uncertainty Quantification
Uncertainty quantification in machine learning involves assessing and managing the uncertainty inherent in model predictions and decisions. Uncertainty can arise from various sources, including noisy data, model assumptions, or the inherent unpredictability of complex systems. Techniques for quantifying uncertainty include Bayesian methods, which provide probabilistic predictions, and ensemble methods, which estimate uncertainty by averaging the predictions of multiple models.
Computational Intelligence for Integrated Design 2/8
WS2: Optimizationlink copied
Optimization is the process of finding the best solution or set of parameters that minimize or maximize a specific objective function, often under a set of constraints.
Topology Optimization
There are many ways to complete topology optimization. Review the tutorial on Topology Optimization with ANSYS. You can also complete topology optimization in Grasshopper with the plug-ins like Topos. If you would like to see an example project that uses topology optimization, take a look at the MSc Thesis Just Glass by Anna Maria Koniari.
Parametric Optimization
There are several different ways to complete optimization in Grasshopper, below are some tutorials to help you get started. These tutorials describe how you can use different Grasshopper plug-ins to analyze single- and multi- objective optimization problems.
The following tutorials use single- and multi- objective optimization to solve a specific design problem
There are also a lot of useful external resourses about optimization methods, such as:

Additional Resources
All optimization tutorials with some additional information about optimization are available on the Optimization subject page.
Computational Intelligence for Integrated Design 3/8
WS 3: Supervised Learning Ilink copied
Supervised learning is a type of machine learning where a model is trained on a labeled dataset, meaning each input has a corresponding known output. The model learns to map inputs to outputs by minimizing the error between its predictions and the true labels, enabling it to make accurate predictions on new, unseen data.
Regression Methods
Multinomial Logistic Regression is an extension of binary logistic regression used for classification problems where the target variable has more than two categories. It models the probability of each category by comparing it to a reference category, using a set of features to predict the likelihood of each possible outcome. The model estimates the probabilities through a set of linear functions applied to the features, ensuring that the sum of the probabilities for all categories equals one.
Bayes Classifiers
Bayes Theorem describes the probability of an event taking place considering prior knowledge about features that might impact the event. Naive Bayes classifiers are based on Bayes theorem and assumes each feature is independent given that the class is known.
K-Nearest Neighbors
To classify inputs using k-nearest neighbors (KNN) classification, it is necessary to have a labeled dataset, the distance metric that should be used to compute the distance between data points, and the value of k which is how many nearest neighbors should be reviewed.
Decision Trees / Random Forest
Decision Trees can provide an efficient classification option when data cannot be separated linearly. The most commonly used decision tree classifier splits the dataset into hyperrectangles with sides parallel to the axes. The tutorial Decision Trees explains the principles with an example. To review an example of Random Forest, take a look at the project Visual Analytics of Jamal van Kastel.
Support Vector Machines
Support Vector Machine creates a decision boundary to separate data into two classes. When determining the decision boundary, multiple decision boundaries can be found that correctly classify the samples. Support Vector Machines try to find the optimal boundary considering the boundary’s distance away from samples.
Computational Intelligence for Integrated Design 4/8
WS 4: Supervised Learning IIlink copied
Supervised learning is a type of machine learning where a model is trained on a labeled dataset, meaning each input has a corresponding known output. The model learns to map inputs to outputs by minimizing the error between its predictions and the true labels, enabling it to make accurate predictions on new, unseen data.
Neural Networks
A feedforward neural network also known as a multi-layer perceptron (MLP), is a neural network with at least three layers: an input layer, a hidden layer, and an output layer. A neural network consists of nodes and the connection between the nodes.
To see applications of Neural Network, you can review the following examples.
Surrogate Models
A surrogate model is a machine learning model that predicts certain performance criteria which allows for a faster analysis than if a simulation was used. Surrogate models can be especially useful when computationally intensive simulations are required or when multiple different simulations or evaluations are being run on the geometry. A surrogate model is trained on simulated data and once trained, it can predict the performance of a new input. There are various machine learning models that can be used for surrogate models which include decision trees, Bayesian networks, and neural networks.
To see applications of Surrogate Models, you can review the following examples.
Thesis: Deep Generative Shell Structure Designs – Pavlidou
Thesis: Deep Generative Truss Structures – Sterrenberg
Paper: Design exploration based on self-organizing map and multi-layered perceptron – Pan et al.
Paper: Highrise daylight optimisation – by Ekici et al.
Paper: Application of Surrogate Models for Building Envelope Design Exploration and Optimization – Yang et al.
Computational Intelligence for Integrated Design 5/8
WS 5: Unsupervised Learninglink copied
Unsupervised learning is a type of machine learning where an algorithm analyzes unlabeled data to identify patterns, structures, or relationships without any explicit guidance or predefined outputs. This approach is commonly used for clustering, dimensionality reduction, and anomaly detection tasks.
Gaussian Mixtures
Gaussian Mixture is a type model corresponding to the probability distribution of a collection of data points within the data set. It is a probabilistic model which assumes that the data points are generated from a mixture of a finite number of Gaussian distributions with unknown parameters.
To see applications of Gaussian Mixture models, you can review the following examples.
Paper: Gaussian Mixture Model for Robust Design Optimization of Planar Steel Frames – Do & Ohsaki
Paper: Growing Gaussian Mixture Regression for Modeling Passive Chilled Beam Systems in Buildings – Wang et al.
Paper: A visualized soundscape prediction model for design processes in urban parks – Yue et al.
Paper: Extended and Generalized Fragility Functions – Andriotis & Papakonstantinou
Clustering – K-Means
K-Means clustering randomly initializes k cluster centroids in the dataset. Then, the algorithm measures the distance between each cluster centroids and each data point in the data set. The distance metric used can be Euclidean or Manhattan distance. The data points are then assigned to the centroids that is closest to that point.
Clustering – Spectral Clustering
Spectral Clustering uses the eigenvalues of the similarity matrix of data to reduce their dimensionality and thus cluster them in a low dimensional manifold. It relates to graph theory and the concept of identifying groups of nodes based on the edges connecting them. Spectral Clustering is useful when the structure of a cluster is highly non-convex, or when a measure of the center and spread of a cluster does not describe a complete cluster. This happens, for example, when clusters are nested circles on a 2D plane.
Clustering – Self-Organizing Maps
A Self Organizing Map (SOM) is a technique used for machine learning that produces a two-dimensional representation of a higher dimensional data set. The goals is to projects the data set into a lower dimension while preserving the original data structure. The data set is separated into clusters of variables with similar values which can be visualized in a map.
To see applications of Self-Organizing Maps, you can review the following examples.
Generative Models
Generative models are statistical models that calculates the probability distribution of a data set given observable variables (variables that can be directly observed or measured) and target variables (dependent variables).
To see applications of Generative Models, you can review the following examples.
Computational Intelligence for Integrated Design 6/8
WS 6: Reinforcement Learninglink copied
Reinforcement learning is a type of machine learning where an agent learns to make decisions by interacting with an environment, receiving feedback in the form of rewards or penalties. Over time, the agent optimizes its actions to maximize cumulative rewards, effectively learning the best strategies through trial and error.
Markov Decision Processes
A Markov Decision Process provides a mathematical framework for modeling decisions that incorporate uncertainty. They are commonly applied in optimization problems.
Value Iteration
Value iteration is a dynamic programming method for finding the optimal value of functions by iteratively solving Bellman equations. It is one method of solving Markov Decision Processes.
Policy Iteration
Policy iteration is one method of solving Markov Decision Processes in which steps are performed consecutively testing different options each time to determine which is most optimal.
Q-Learning
Q-learning is an algorithm used in reinforcement learning that finds an optimal policy for a finite Markov decision process. The policy determines the optimal action to take at each time step.
To see applications of Q-Learning, you can review the following examples.
Computational Intelligence for Integrated Design 7/8
Supplemental Materialslink copied
Digipedia
Digipedia has tutorials on a wide range of topics. Use the Subjects and Software pages to navigate to tutorials that may not be linked here including some for ANSYS, Gallapagos, Honeybee and Ladybug, Karamba3D, Wallacei, and many others.
Jupyter Notebooks and Python
At the workshops, you will be using Jupyter notebooks to apply one or more of the methods discussed in the lecture. For the workshop, please ensure please ensure you have Python, Jupyter, and Scikit Learn installed. You can follow the tutorial to do so.
Grasshopper Plug-Ins
You do not need to know how to code to apply machine learning in your project. Once you understand the concepts covered in the course, you can apply them in Grasshopper using various plug-ins.
Data Sets and Data Processing
Machine learning relies on data. The quality and quantity of data that is available and used for training and testing a machine learning model, have a big impact on the performance of the trained model. The source of data can vary and can include being collected by researchers for a project or using an existing data set. The format of data sets also vary and can include spreadsheets and databases. The following tutorials provide additional information on data sets and data preprocessing.
Data streams across Grasshopper and Jupyter Notebooks
Using Grasshopper plug-ins, it is possible to work with machine learning methods only in Grasshopper. If you would like to use some of the code we have demonstrated in the Jupyter notebooks, you may need to create data in Grasshopper, import it in a Jupyter notebook, and then transfer it back.
Application Examples
We have provided summaries of various machine learning applications in the architecture, engineering, and construction domain. These examples are all located on the examples page.
Computational Intelligence for Integrated Design 8/8
Past Course Projectslink copied
Below is a selection of past projects you can review if interested.
2024
The links below show examples of past projects completed in this course.
Write your feedback.
Write your feedback on "Computational Intelligence for Integrated Design"".
If you're providing a specific feedback to a part of the chapter, mention which part (text, image, or video) that you have specific feedback for."Thank your for your feedback.
Your feedback has been submitted successfully and is now awaiting review. We appreciate your input and will ensure it aligns with our guidelines before it’s published.
