WV4 Line 1 – Workshop 4 – Dataset analysis with Clustering:
-
Intro
-
Clustering
-
Clustering high-dimensional data
Information
| Primary software used | Python |
| Software version | 1.0 |
| Course | WV4 Line 1 – Workshop 4 – Dataset analysis with Clustering: |
| Primary subject | AI & ML |
| Secondary subject | Machine Learning |
| Level | Intermediate |
| Last updated | November 27, 2024 |
| Keywords |
Responsible
| Teachers | |
| Faculty |
WV4 Line 1 – Workshop 4 – Dataset analysis with Clustering: 0/2
WV4 Line 1 – Workshop 4 – Dataset analysis with Clustering:
Discription of clustering terminology.
This workshop introduces unsupervised learning methods to extract patterns from unlabelled datasets. It demonstrates using clustering algorithms to capture similarities between data points and group them accordingly.
Clustering can be used to answer exploratory research questions like: can we identify different types of households based on housing preferences and living conditions?
Exploratory questions are exploratory because the research aims to uncover patterns, structures, or relationships in data that are unknown, rather than testing a specific hypothesis.
WV4 Line 1 – Workshop 4 – Dataset analysis with Clustering: 1/2
Clusteringlink copied
Clustering is an unsupervised learning technique to find groups (clusters) of similar data points within a dataset. Unlike classification, clustering does not use labelled data. However, similarly to classification clustering aims at finding the decision boundary separating data points.
In classification, a data point is represented by (1) a set of features and (2) the corresponding class or label. Supervised learning methods are then used to learn a function that approximates the mapping from features to labels. In clustering, a data point is represented by a set of features only. Unsupervised learning methods are used to compare data points and identify classes based on the data points’ similarity.
Clustering works as follows. A certain number of points (R), not part of the dataset and each representing the centroid of a cluster are spread over the feature space. Then, the classification of a data point is made to the class of the closest centroid. The proximity is generally measured as the Euclidean distance in the feature space after each feature has been standardised.
Euclidean distance
The Euclidean distance between two data points P = (p1, p2, …, pn) and Q = (q1, q2, …, qn) in an n-dimensional space is defined as a straight line between them. The formula is:
In simpler terms, the Euclidean distance is the square root of the sum of the squared differences between the corresponding coordinates of the two points.
The K-means algorithm
The main challenge in clustering is identifying the number and position of cluster centroids in the feature space. There are many different methods to do so.
K-means clustering is a method for finding clusters and cluster centres in unlabelled data. You select the number of clusters, say R, and the algorithm iteratively moves the centres to minimise the total within-cluster variance (the sum of squared distances between data points and their nearest centre).
The k-means clustering process involves two-steps:
- Assigning data points to clusters: for each centre, we identify the subset of data points (its cluster) closer to it than any other centre.
- Updating cluster centres: for each cluster, we compute the means of each feature for each data point, and this mean vector becomes the new centre for that cluster.
These two steps are repeated until the algorithm converges, meaning the cluster centres no longer move significantly.
Figure below shows an application of the K-means algorithm to cluster data samples represented by two features. In this case, the data points naturally form three distinct clusters, which allows the clustering process to converge quickly. The straight lines show the partitioning of points, each sector being the set of points closest to each centroid.
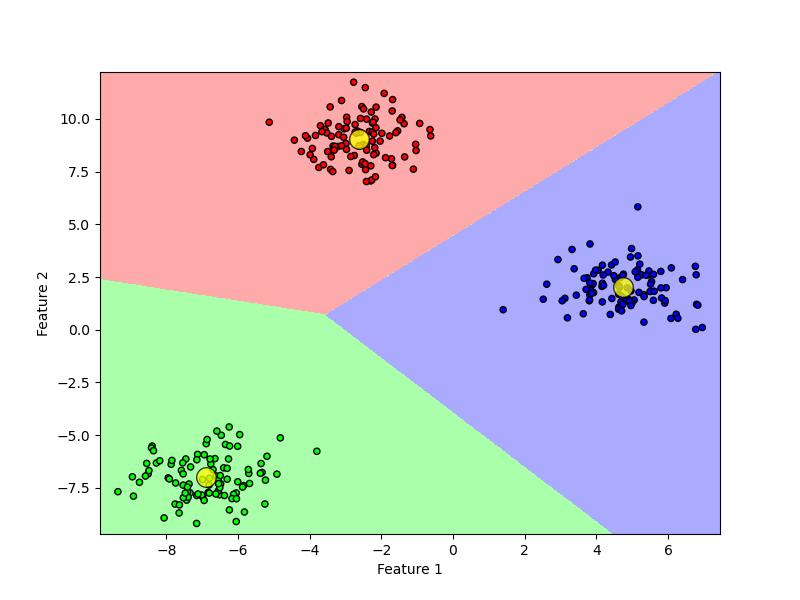
In a 2D example like this clustering could be achieved through visual inspection without a machine learning algorithm. However, for high-dimensional datasets or more complex data distributions, K-means can be useful for exploring potential patterns or ‘types’ of data that may emerge based solely on the feature set.
Note: Similarly to classification, once you have trained a K-means model and found the cluster centroids, you can use the model to assign new data points to one of the existing clusters.
Example A: Clustering data in 2D
To get a better understanding on how clustering works you should follow this simplified example of classifying random points. In the exercise you quickly generate your own dataset of points and cluster the points by using a k-means clustering to cluster the data into a specified number of clusters. You will learn how to plot the regions of each cluster and analyse the clusters visually. Additionally, the effects of different initialisation methods and selecting different number of clusters is discussed.
Debate A: Clustering
If you are following this tutorial because you are attending the course BK3WV4, after you have learned the theory and practiced the exercises, you will attend a workshop in class at TU Delft. The workshop lasts 3 hours. During the workshop, you will work with the tutors. Two hours are contact hours with your tutor and one hour is for activities without tutors. During the first one hour, you will discuss the tutorial with the tutor and your classmates. During the second hour, you will write a first draft of your workshop deliverable. During the third and fourth hour, you will discuss how the content of the workshop relates to your research question.
- How would you use clustering to answer your research question?
- Which data features would you select to run a clustering algorithm?
WV4 Line 1 – Workshop 4 – Dataset analysis with Clustering: 2/2
Clustering high-dimensional datalink copied
High-dimensional data
Clustering high-dimensional data is more challenging because the distance between data points becomes less meaningful as the number of features increases. High-dimensional clustering typically requires dimensionality reduction to project the data into a lower-dimensional space while preserving the important relationships between data points.
Dimensionality reduction
PCA (Principal Component Analysis) and t-SNE (t-Distributed Stochastic Neighbor Embedding) are common techniques for reducing high-dimensional data. These techniques can be used to:
- reduce the dimensionality of data points before clustering to improve the performance of the ML model
- reduce the dimensionality of data points after clustering (2 or 3 dimensions) to visualise the results of the clustering process.
Exercise B: Clustering of N-D Data with WoOn Dataset
If you want to put the learned terminology to practice with a real-world problem you should follow this exercise. In this exercise you will use the WoON21 dataset to create clusters based on distance-related features by running K-Means clustering.
Debate B: Clustering high-dimensional data
If you are following this tutorial because you are attending the course BK3WV4, after you have learned the theory and practiced the exercises, you will attend a workshop in class at TU Delft. The workshop lasts 3 hours. During the workshop, you will work with the tutors. Two hours are contact hours with your tutor and one hour is for activities without tutors. During the first one hour, you will discuss the tutorial with the tutor and your classmates. During the second hour, you will write a first draft of your workshop deliverable. During the third and fourth hour, you will discuss how the content of the workshop relates to your research question.
- Assuming you wanted to extract ‘types’ (clusters) from your data. How many types would you look for and why?
- Which features would you select to represent your data points for clustering and why?
Write your feedback.
Write your feedback on "WV4 Line 1 – Workshop 4 – Dataset analysis with Clustering:"".
If you're providing a specific feedback to a part of the chapter, mention which part (text, image, or video) that you have specific feedback for."Thank your for your feedback.
Your feedback has been submitted successfully and is now awaiting review. We appreciate your input and will ensure it aligns with our guidelines before it’s published.
