WV4 Line 2 – Workshop 3: Optimisation
-
Intro
-
Selecting objectives
-
Multi-objective optimization methods
Information
| Primary software used | Grasshopper |
| Course | BKB3WV4 – Bouwkunde als wetenschap |
| Primary subject | AI & ML |
| Level | Intermediate |
| Last updated | November 27, 2024 |
| Keywords |
Responsible
| Teachers | |
| Faculty |
WV4 Line 2 – Workshop 3: Optimisation 0/2
WV4 Line 2 – Workshop 3: Optimisation
This tutorial explains how to select variables and objectives for the optimization for research and explains the different optimization methods.
This workshop provides you with the basic concepts and terminology you use in Workshop 3. The workshop 3 explains how to select variables and objectives for the optimization for research and explains the different optimization methods. The first section of this workshop explains how to select variables and objectives in a sensible way. The second section of this workshop explains different optimization methods.
WV4 Line 2 – Workshop 3: Optimisation 1/2
Selecting objectiveslink copied
Optimization describes the process of searching for possible solutions until no better solution can be found. The quality of the solution is evaluated based on an objective. The feasible solutions are found by exploring the possible combinations of the features.
Objective:
are the performance indicators minimized or maximized during the optimization process (e.g. a daylight factor to be maximized; the weight of the structure to be minimized; solar gain to be either minimized or maximized; etc.)
Variables:
Variables are typically the aspects of the problem that can be adjusted by the optimization algorithm to find the optimal solution. They are the variables defining the solution space. These are continuously updated during the optimization process (e.g. your sliders in GH if you use GH).
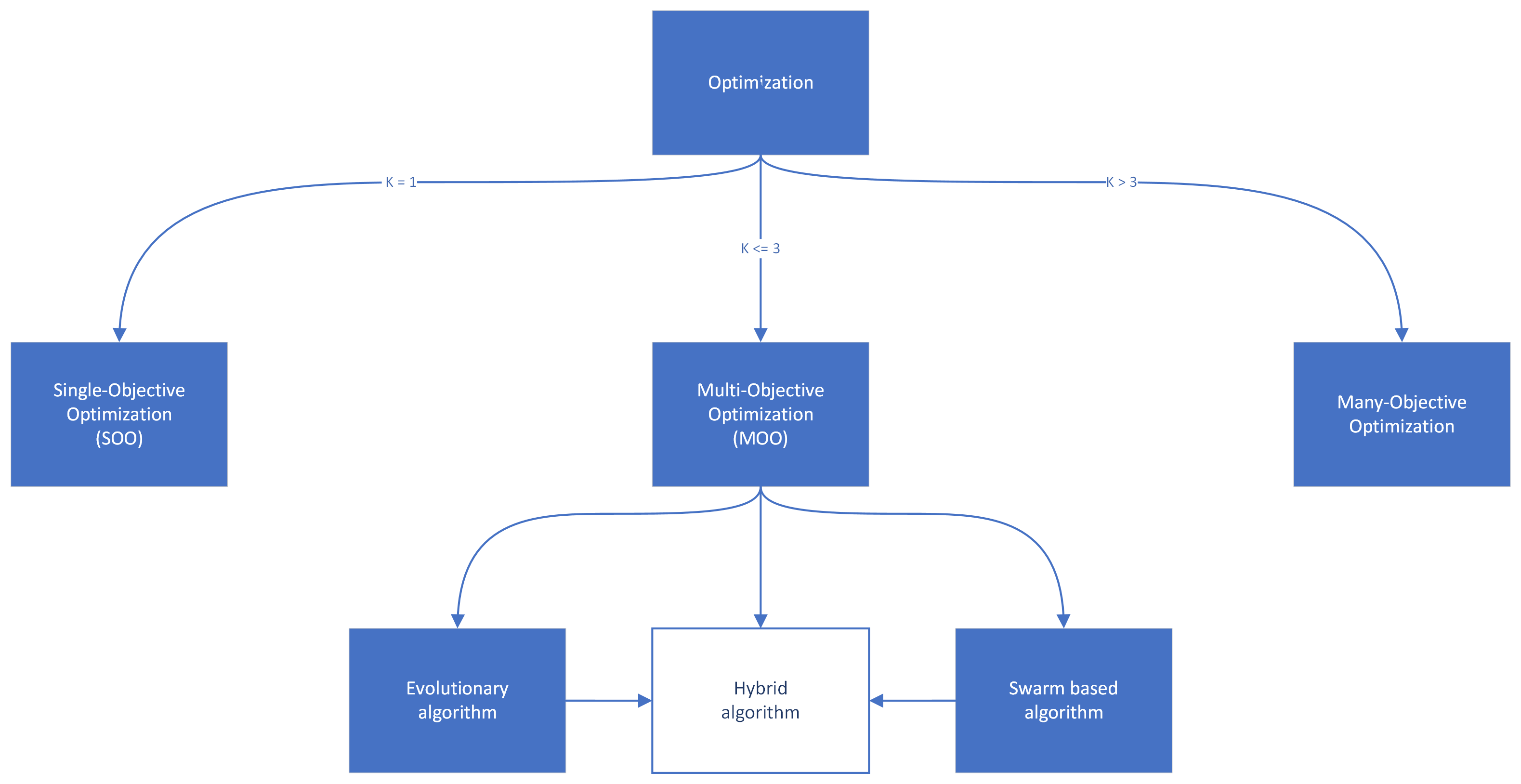
Types of optimization problems – nr of objectives
There are different types of optimizations problems, when categorizing them by the number of objectives. Firstly, they can be grouped depending on the number of objectives selected for the optimization problem. The categories are, single objective optimization with 1 objective, multi-objective optimization with 2 or 3 objectives, and many-objective optimization with 4 or more objectives.
Single-objective optimization
In single-objective optimization usually a single solution is obtained.
Multi-objective optimization
In multi-objective optimization there is no direct method to determine if one solution is better than another, because the outcome is a set of solutions that involve multiple conflicting objectives considered simultaneously. With multi-objective optimization there is not 1 optimal solution, as the improvement of one objective leads to the degradation of another objective, but a set of trade-off solutions representing the compromise between the conflicting objectives.
Many-objective optimization
The goal of many-objective optimization problems is to find a set of solutions that are the best trade-off among the objectives. Many-objective optimization problems consist of 4 or more objectives, making the problem high dimensional.
Example papers
The following papers give a clear explanation on how the discussed terminology can be used during research. We highly recommend you to look at these papers.
A generative façade design method on daylight performance goals – Gagne and Andersen, 2012
- ResearchGate Article by Gagne and Anderson 2012
- Clear explanation of optimization objectives
- Clear overview of variables and constraints of model
- GA algorithm validation of simplified shape
- Straight forward optimization results, so easy to understand the principle
- Visualization on pareto front with design options
Debate A: Selecting objectives
If you are following this tutorial because you are attending the course BK3WV4, after you have learned the theory and practiced the exercises, you will attend a workshop in class at TU Delft. The workshop lasts 3 hours. During the workshop, you will work with the tutors. Two hours are contact hours with your tutor and one hour is for activities without tutors. During the first one hour, you will discuss the tutorial with the tutor and your classmates. During the second hour, you will write a first draft of your workshop deliverable. During the third and fourth hour, you will discuss how the content of the workshop relates to your research question.
- For your research topic what could the variables for an optimization? Give information about constraints, set sizes etc. and argument why you select these based on your research boundaries.
- For your research topic what could the objectives for an optimization?
- How do the objectives relate to the research question(s)?
- What type of objectives are they? Argument for each objective if and why you’re minimizing, maximizing, or using a closest value, constraint or domain.
WV4 Line 2 – Workshop 3: Optimisation 2/2
Multi-objective optimization methodslink copied
Multi-objective techniques can be categorised into different classes, the two main classes are evolutionary and swarm-based techniques.
Evolutionary Algorithms (EA)
Evolutionary techniques use the concepts of natural evolution, and mimics the selection and reproduction process of living organisms. Evolutionary techniques uses a population, fitness function and genetic operations.
The population is a set individual solutions for the optimization problem. The fitness function measures how well a solution solves the optimization problem. Genetic operations create new populations. The main used genetic operators are mutation (random changes), crossover (combining parts of two solutions), and selection (selecting best solutions) to evolve solutions into new generations.
The workflow for evolutionary algorithms is as follows. First, an initial population of random solutions is randomly generated. Then, the population is evaluated based on the fitness function. Then, based on their fitness individuals are selected to participate in reproduction. During the reproduction a new population is created with the help of genetic operators creating new individuals. Then the loops starts again from the second step, evaluation and continues until the termination condition is met.
If you’re interested to learn more about the evolutionary operators you can watch this video:

The evolutionary algorithms can be categorised based on the strategies the algorithm uses. The main used strategy is dominance-based, and uses the concept of Pareto dominance to evaluate and select solutions. A solution dominates another solution if the solution is at least as good in all objectives and better in at least one objective. The pareto-based strategy is explain in the next workshop. One of the well-known example of dominance-based evolutionary algorithms is NSGA-II (Non-dominated Sorting Genetic Algorithm II), which mainly uses crossover and mutation operations during reproduction.
Swarm-based techniques
Swarm-based algorithms use the concept of collective behaviour of decentralized, self-organised systems. In other words, swarm-based algorithms mimic the collective behaviour of social animals. The basic concept originates from a study on the behaviour of birds.
The workflow for swarm-based algorithms is as follows. First, an initial population of random solutions is randomly generated in the solution space. Then, the population is evaluated based on the fitness function. Based on the evaluation, the personal best of each solution and the local/global best solution in the iteration is found. Then, the position of the solution in the solution space is updated based on their own best personal solutions and the best local/global solution in the iteration. Then the loops starts again from the second step, evaluation and continues until the termination condition is met.

The most known swarm-based optimization algorithms are: Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Artificial Bee Colony (ABC), Differential Evolution (DE), and Grey Wolf Optimization (GWO).
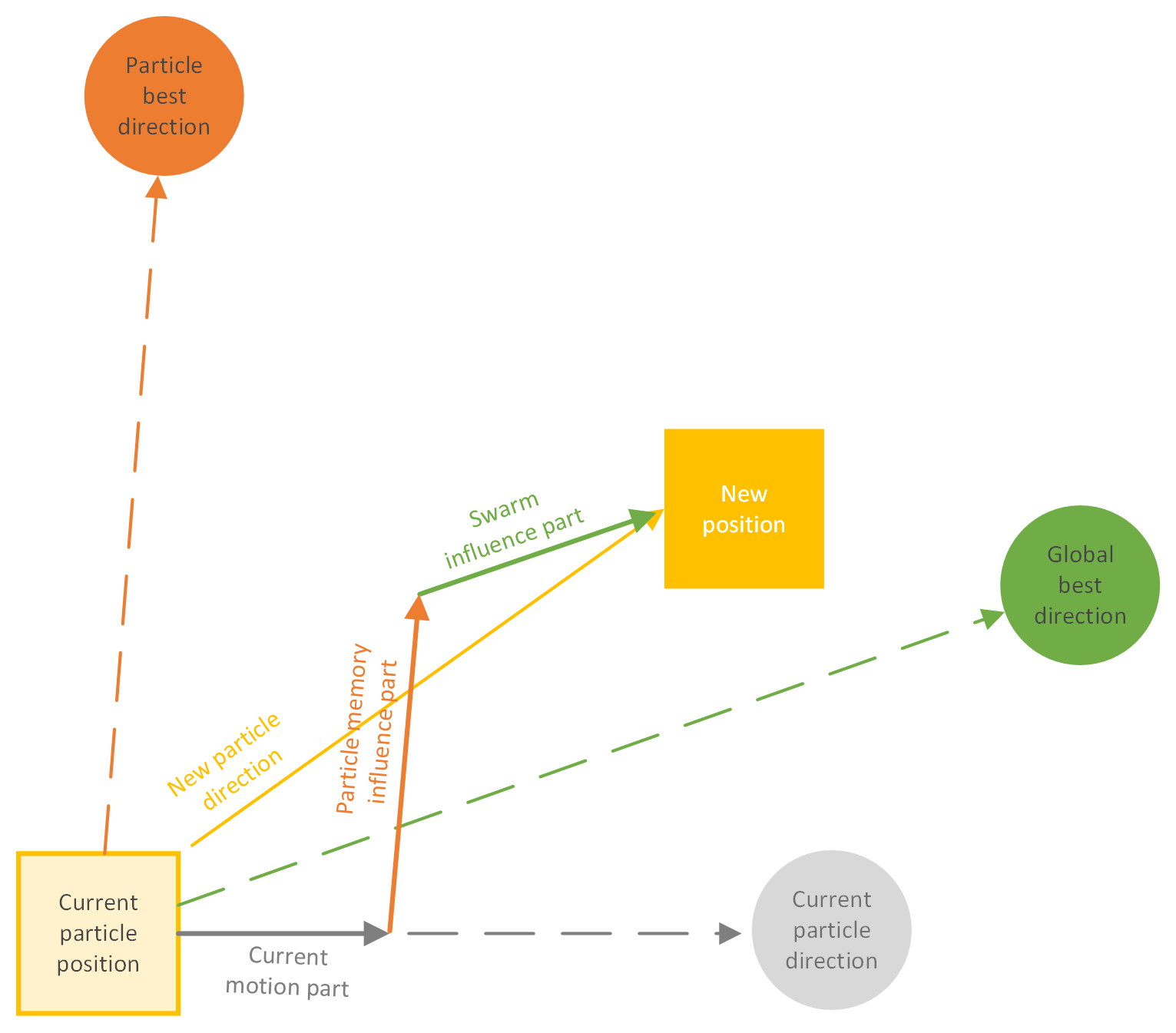
The particle swarm algorithm is a popular swam-based algorithm inspired by bird flocking or fish schooling. The main idea is that individuals (particles) benefit from the experience of other individuals in the group.
The new position of a particle is influenced by three aspects. The current motion of the particle, the particle best direction, and the global best direction. The concept of updating a particle position of particle swarm optimization algorithm is shown in Figure X.
Many objectives and evolutionary techniques
Multi-objectives evolutionary techniques are designed to handle up to 3 objectives, using these techniques for many-objective problems (>3 objectives) could cause problems that relate to the inefficiency of selection operators, high computational cost and difficulty in visualizing the objective space. The visualization of many-objective problems is difficult, which makes the decision making more difficult. The Pareto Front takes different forms depending on the number of objectives. A 2-objective problem results in a curve, while a 3-objectiveproblem results in a surface. As the number of objectives are 4 or higher, the Pareto Front could be represented by a hypersurface or a higher-dimensional shape. Therefore, the number of solutions increase exponentially with the number of objectives in the optimization problem. When more than 3 objectives are involved in the optimization problem it could result in a poor Pareto-optimal front as almost all solutions in the population become non-dominant to each other.
Example: Running an MO-Optimisation
To get a better understanding on how to set-up a parametric model for an optimization process and selecting the right objectives with constraints, you should follow this exercise. In the exercise you will work with a façade with panels, where you want to optimize the placement of a window for optimal panel placement in the facade.
Example papers
The following papers give a clear explanation on how the discussed terminology can be used during research. We highly recommend you to look at these papers.
Shape optimization of concrete floor systems for sustainability, acoustical, and thermal objectives – Broyles et. al.
- ResearchGate Article by Broyles et al., 2022
- Visual explanation of parametric model and variables of a structural topic
- Multiple different graphs to discuss the results
- Pareto front with corresponding results
- Parallel coordinate plot per solution
- Gives an example of constrained optimization
- Application of research in design with visual results
Debate B: Optimization methods
If you are following this tutorial because you are attending the course BK3WV4, after you have learned the theory and practiced the exercises, you will attend a workshop in class at TU Delft. The workshop lasts 3 hours. During the workshop, you will work with the tutors. Two hours are contact hours with your tutor and one hour is for activities without tutors. During the first one hour, you will discuss the tutorial with the tutor and your classmates. During the second hour, you will write a first draft of your workshop deliverable. During the third and fourth hour, you will discuss how the content of the workshop relates to your research question.
- If you would have to lower the number of objectives for the optimization how would you do it?
- Create an example in relation with your research topic where you would have 4 objectives, how would you bring this down to 3 objectives?
Write your feedback.
Write your feedback on "WV4 Line 2 – Workshop 3: Optimisation"".
If you're providing a specific feedback to a part of the chapter, mention which part (text, image, or video) that you have specific feedback for."Thank your for your feedback.
Your feedback has been submitted successfully and is now awaiting review. We appreciate your input and will ensure it aligns with our guidelines before it’s published.
