Transformations in Grasshopper
-
Intro
-
Move
-
Rotate
-
Scale
-
Conclusion
Information
| Primary software used | Rhino |
| Course | Transformations in Grasshopper |
| Primary subject | Parametric Modeling |
| Secondary subject | 3D modelling |
| Level | Beginner |
| Last updated | November 29, 2024 |
| Keywords |
Responsible
| Teacher | |
| Faculty |
Transformations in Grasshopper 0/4
Transformations in Grasshopper
In this tutorial you will learn how to transform your geometry in Grasshopper.
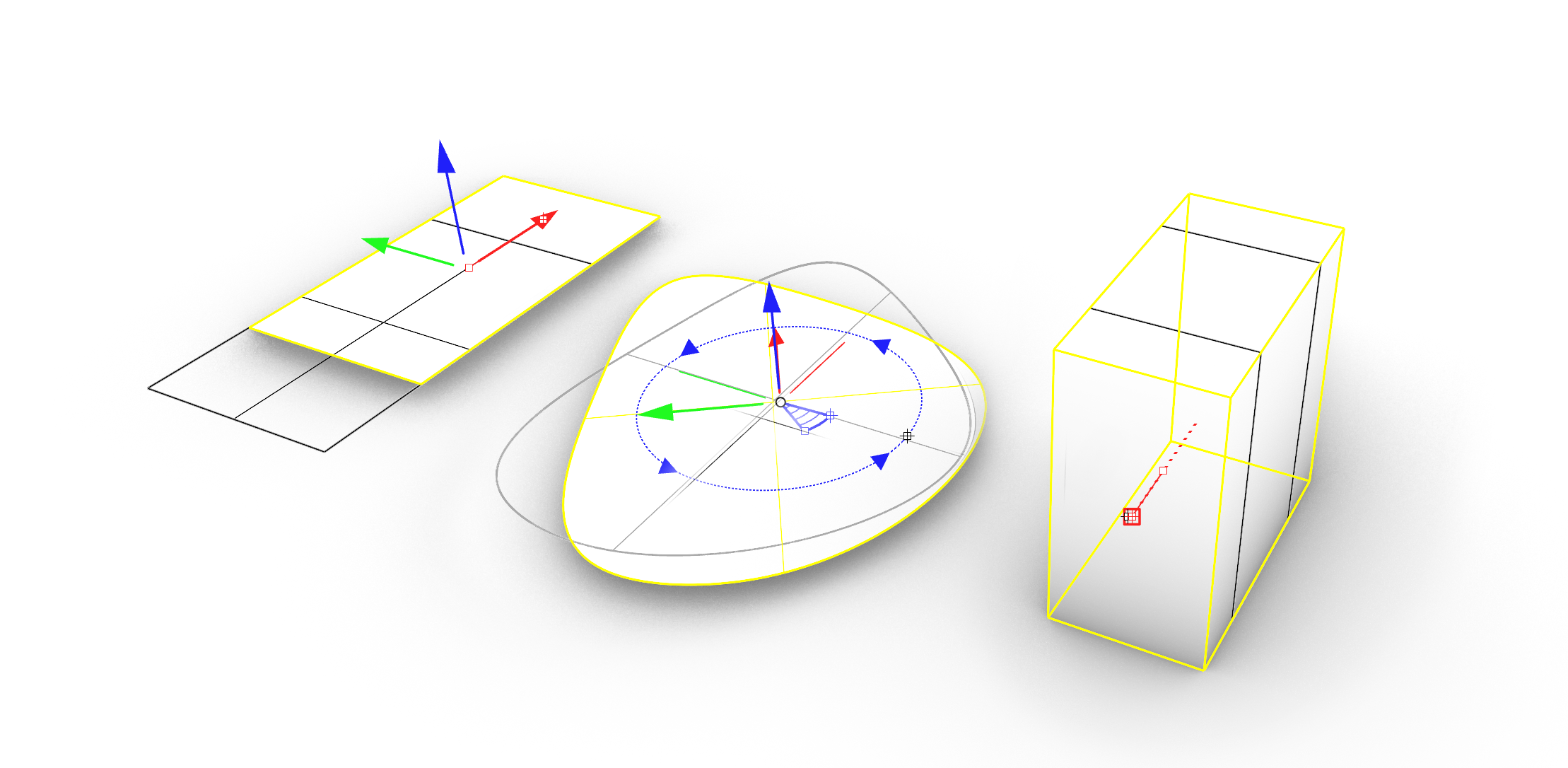
Transformations are the basic alterations which you can apply on your geometry. It contains
- Move
- Rotate
- Scale
Because we don’t have a mouse input in Grasshopper the Transformations need information about for example: the direction of movement, distance of movement, rotational axis or plane and scale origin point.
The principle of Transforming geometry is similar with all options. It consists in principle on 3 inputs:
- Geometry input: Geometry which has to be transformed.
- Value input: Amount of transformation.
- A Point, Line, Plane or Vector input : Defining the location and direction of the transformation.
The last option can vary depending on the selected Transformation. The first two inputs speak for themselves. The last input requires a Point, Line, Plane or Vector input. There are 3 methods for defining these inputs.
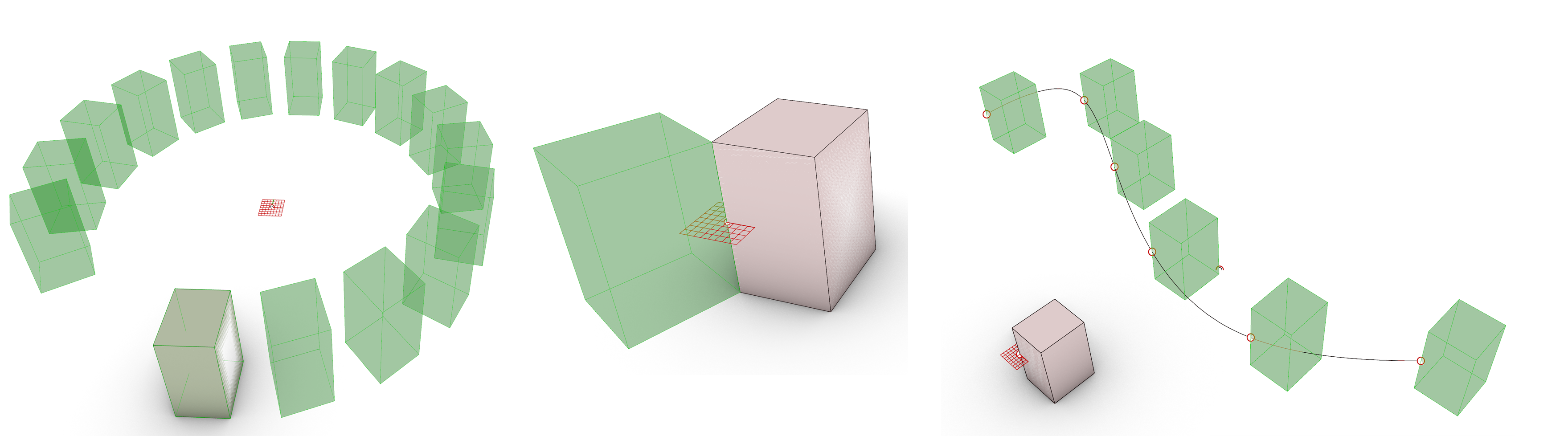
- You can create these inputs yourself in Rhino or Grasshopper. In that case these inputs are not connected to other geometry and will behave as independent inputs which might not be ideal if the Transformation is relative to the geometry. Think about a lamella being rotated. If the rotational axis is generated independent of the lamella any change of amount of lamellas will lead to wrong rotation of the lamella. The position of the lamella doesn’t align anymore with the rotational axis.
- Extract the information from the object and/or related objects which will be transformed. In that case we use the Curve/Surface analysis options. These options allow us to extract the needed input for the Transformation. The advantage is that if the surface/curve changes the extracted information from the input will automatically updated. The relation is parametric. In the case of the lamella, we can extract an edge from the lamella and use this as rotational axis. Changing the location of the lamella will have no influence on the rotation. If you search for a certain input, just drop the analysis options on your canvas an look for the option with the correct output.
- The third option is the creation of divisions of surfaces and curves or grids. This can generate a series of points and planes which can be used for the transformations. In the case of the lamella we can use a divided curve generating a series of points to move the lamella to these points on the curve .
Transformations in Grasshopper 1/4
Movelink copied
If we want to move an object we have to define the direction and the distance of movement.
This can be done in two ways:
- Use an vector
- Displacement from point to point
- Displacement from plane to plane (orient option)
Move using a vector
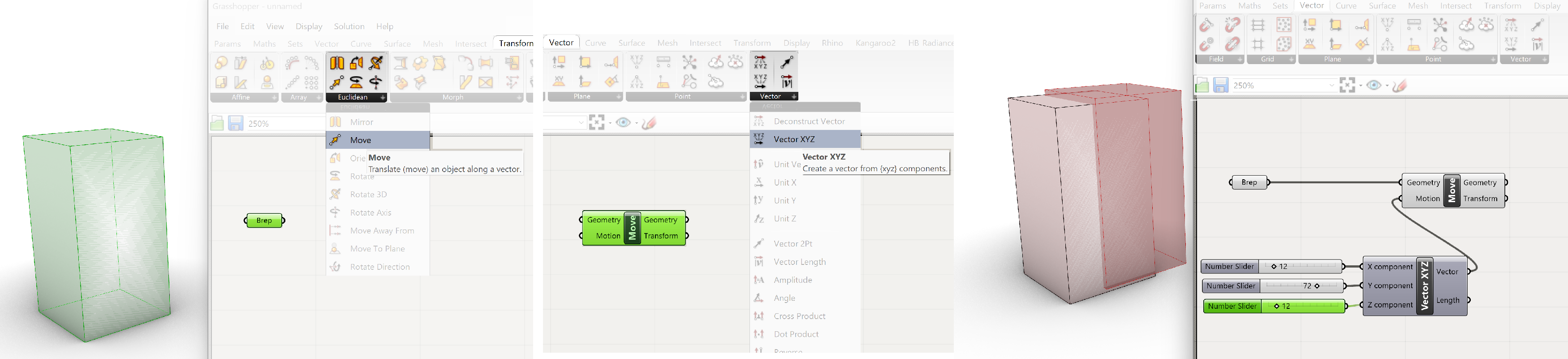
The most basic form of moving an object in Grasshopper is with the use of a vector. The vector defines the direction and distance of movement. The movement is relative. There are several ways on how to apply a vector. You can construct one or use a predefined direction.
To construct a vector go to Grasshopper and select Vector XYZ. This component allows you to define the displacement of an object with an X,Y and Z value. The values can be defined by a number slider. Double click on the canvas and type in a number this will generate a number slider.
Vector >> Vector>> Vector XYZ.
Select from the Transform tab in Grasshopper the Move component. The move component has two inputs: The object you want to move and the direction and distance of movement. Connect the parameter which contains the object to the Geometry input and the Vector XYZ component to the Motion input.
Transform>>Euclidian>>Move.
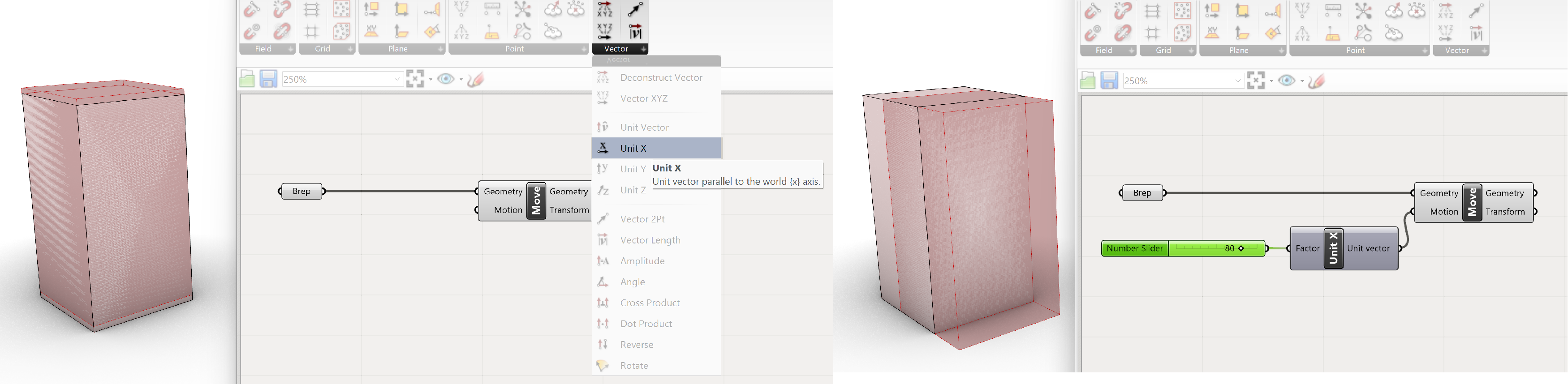
A simpler version of defining the direction is the use of a predefined direction of a Vector. These vectors are called Unit X, Unit Y and Unit Z and have a besides the definition of the direction of X, Y and Z axis a standard distance of 1. By adding a number slider to the Unit X for example that number can be changed into the required distance.
Vector>>Vector>>Unit X
Displacement from point to point
The displacement from point to point is especially useful when want to move an object onto another object. To make this work we need to create two points. These points can be on or in the object you want to move and on or in the target object. These points will define the start point and the target point.
These points can be extracted from the geometry which you want to move and from the target geometry. How to extract a point from an object depends on the type of object. Extracting a point from a surface is different than from a curve. To tackle both we will move a surface to a curve.
Note: Be aware that if you created a solid like a box the options for extracting a point for a surface won’t work because the box is a solid, not a surface. To negate that problem you can explode the box and add the separate surfaces to a surface parameter.
Extracting a point from a surface:
The box is exploded and the separate surfaces are added to a surface parameter. To extract a point form the surfaces we go to Surface, Analyses, Evaluate Surface and add the component. The component has two inputs: Surface and point.
Surface>>Analyses>>Evaluate Surface
Point refers to the U and V coordinates on the surfaces. Each surface created in Grasshopper and Rhino has its own coordinate system which follows the surface of the object. They are independent of the world coordinate system of X,Y and Z coordinates. A surface has the coordinates U and V, This is called an object coordinate system.
The surface parameter can be connected to the Surface input of the Evaluate Surface component.
For the point input we create a point:
Vector>>Point>>Construct Point.
The reason why we can use a construct point for defining a coordinate on a surface has to do with the similarity of input of X,Y and Z for world space coordinate system to the U,V,W object coordinates space system.
We couple the point component to the point input of the Construct Point component. A set of number sliders connected to the X and Y input will define the U and V coordinates on the surface. These coordinates can be defined by the length and width of the surface in for example millimeters. However there is an option to force the length and width to the maximum value of 1, this is called parameterizing. This can be quite useful if you want to define the surface coordinates in equal segments, like 0.2,0.4,0.6,0.8,1.0.
For this example we parameterize the surface, changing the coordinates to a value between 0 and 1.
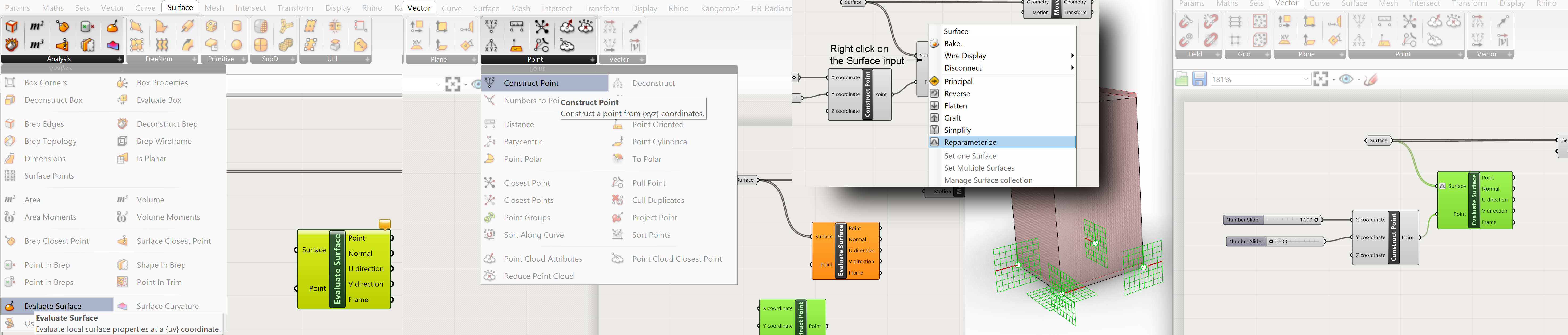
We have now a not one point but 6 points. 1 point for each of the 6 surfaces defining the box. We have to select on point from the 6 points. If we put a Panel to the output of the Evaluate Surface component we can see that there are 6 points in the list.
Parameter>>Input>>Panel
We use a List Item component to make the selection. Connect the point output of the Evaluate Surface component to the List input of the List Item component. The index input of the Evaluate Surface component allows you to select the point you want to use as starting point for the move. You can use a number slider for this input.
Sets>>List>>List Item
For the target we going to use a point on a curve.
Create a curve in Rhino (or in Grasshopper) and connect it to a Curve parameter.
Parameter>> Geometry>> Curve parameter
To define a point a point on the curve we use Point on Curve. This option allows to define a point on the curve with values between 0 and 1 and thereby automatically reparametrizes the curve from length information in for example millimeters to an absolute value between 0 and 1.
Curve>>Analysis>>Point on Curve
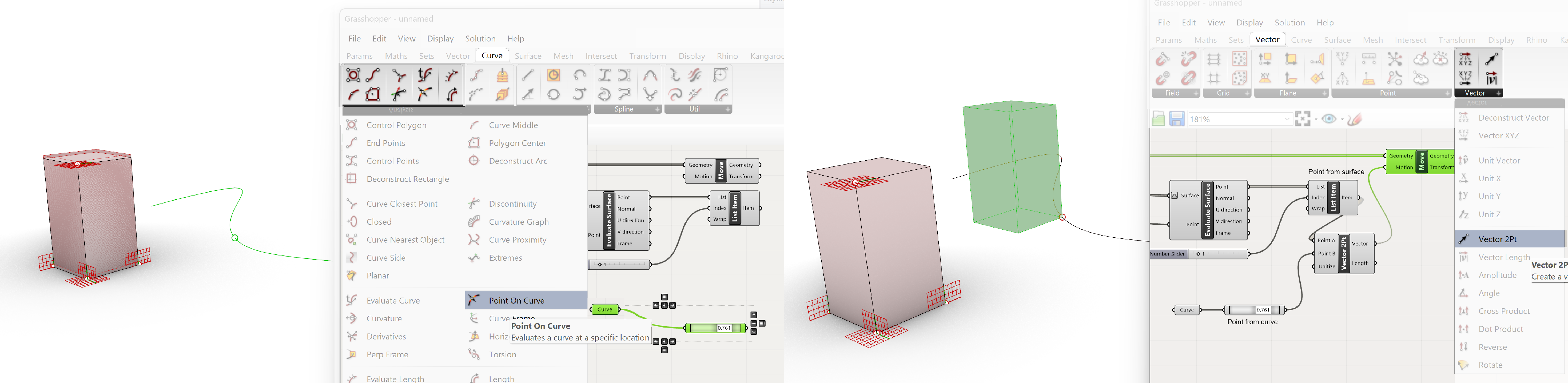
We have now 2 points and can define the movement. We will use the two points to create a vector between the two points. We add Vector 2PT and connect the selected point from the surface to the Point A input of the Vector 2PT component and the selected point from the curve to the input of the Point B input of the Vector 2PT component.
Vector>>Vector>>Vector 2PT
Although the option of moving an object from point to point might look more complex than a movement with an vector, it allows for some powerful options.
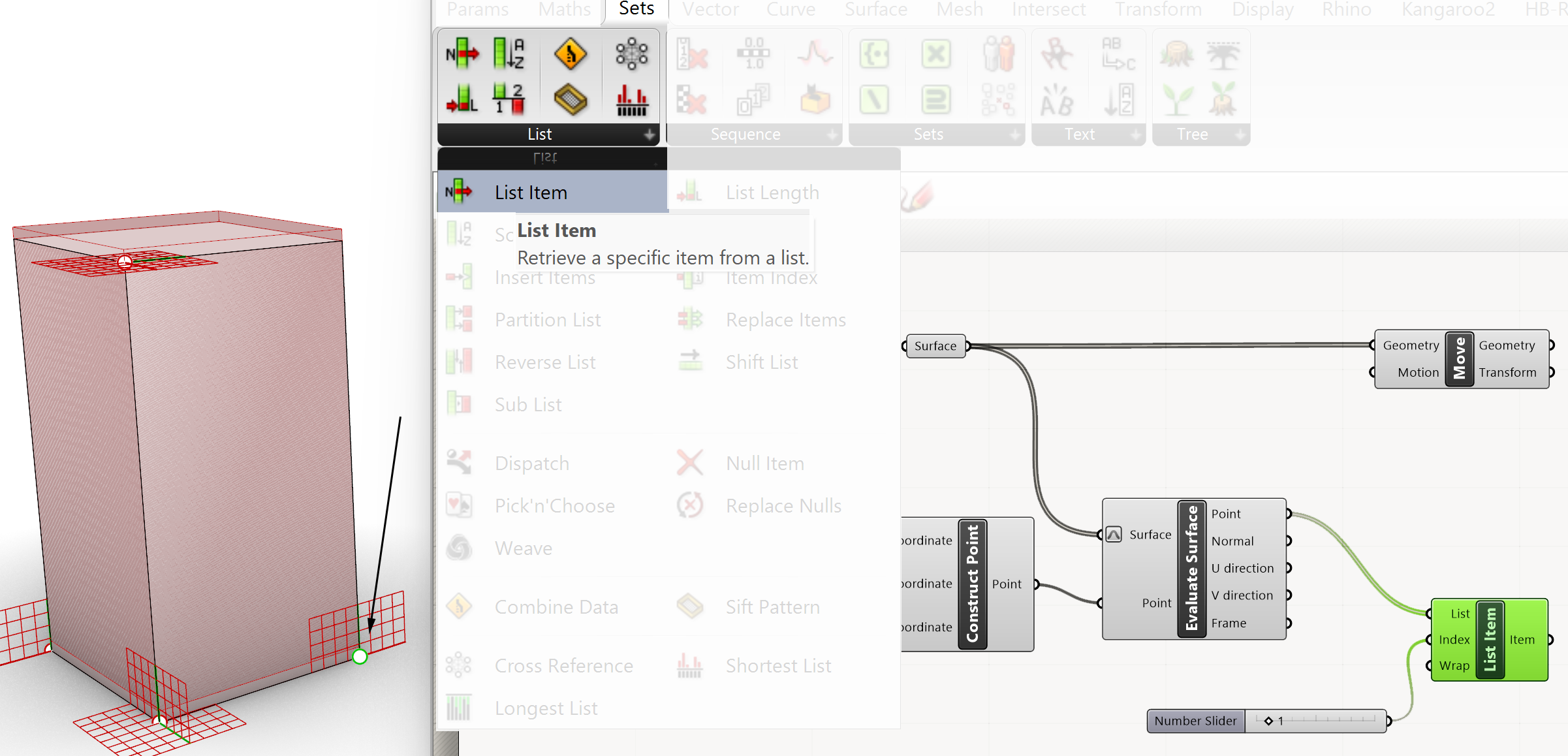
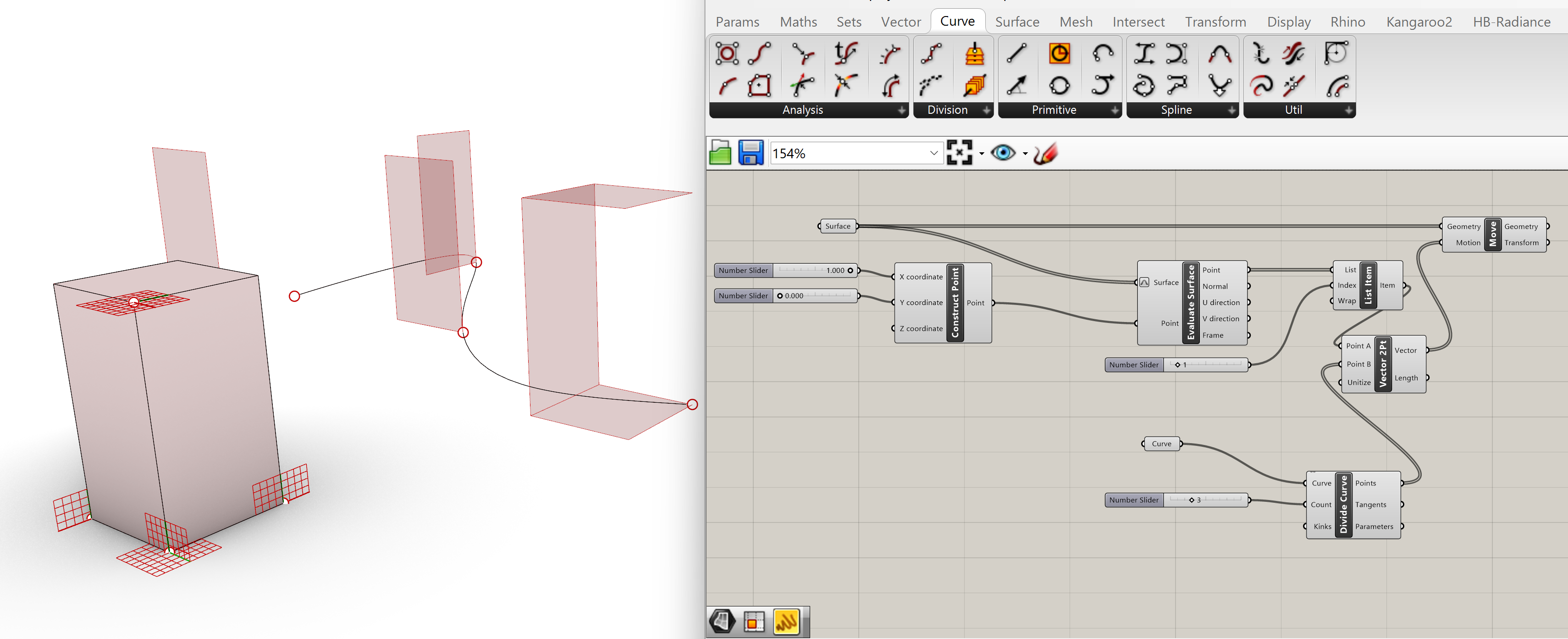
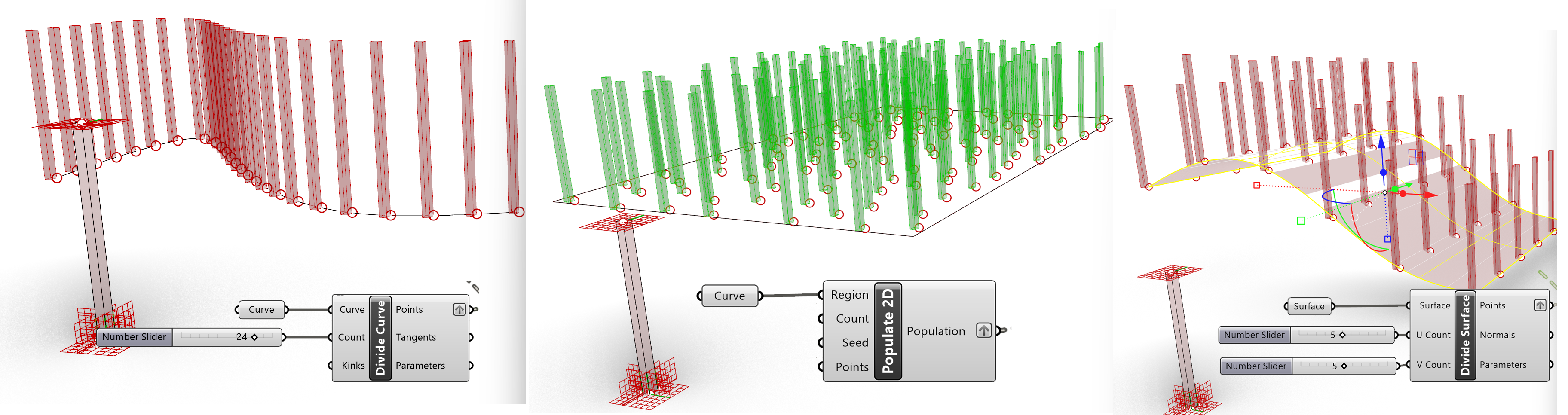
Moving an object to multiple target points. If we divide the curve in multiple segments we can generate multiple points on a curve. To divide the curve we can use the Divide Curve.
Curve>>Division>>Divide Curve.
Couple the Curve output to the Curve input of the Divide Curve component. Connect a number slider to the Count input of the Divide Curve component, this will dictate the amount of divisions and points on the curve.
Now something weird is happening. The box is separated into its separate surfaces and distributed along the curve. This is the result of an important feature of Grasshopper. If you have a list with 6 surfaces, the sides of the box , like we have in this example and we have a list of 4 points of a curve the lists will interact in a very specific way. This interaction is one of the most powerful options in Grasshopper, however it can be quite a challenge to get working correctly. Because the box is a collection of 6 surfaces we have a list of 6 surfaces defining the box. If we want to move the surfaces, the list of target points works at follows.
The first target point in the list will be assigned to the first surface in the list, the second target point in the list to the second surface in the list. Same for the third and fourth target point. However we have more surfaces then target point. Grasshopper solves this in the following way. It assigns the last target point to the rest of the surfaces. That explains why you see 3 separate and 1 combined set of 3 surfaces.
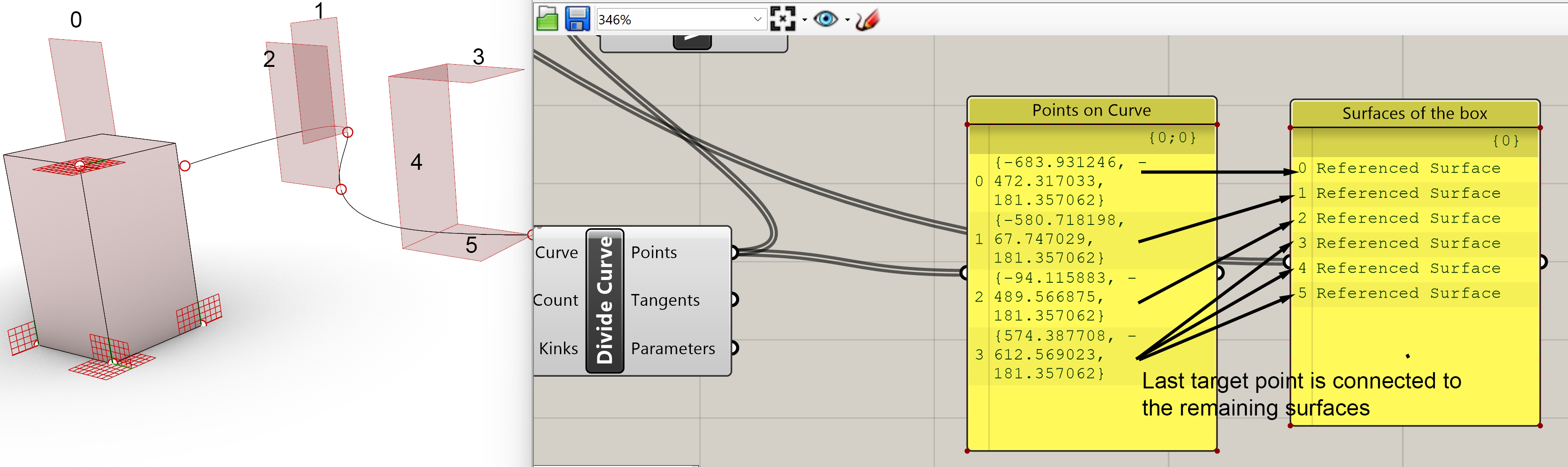
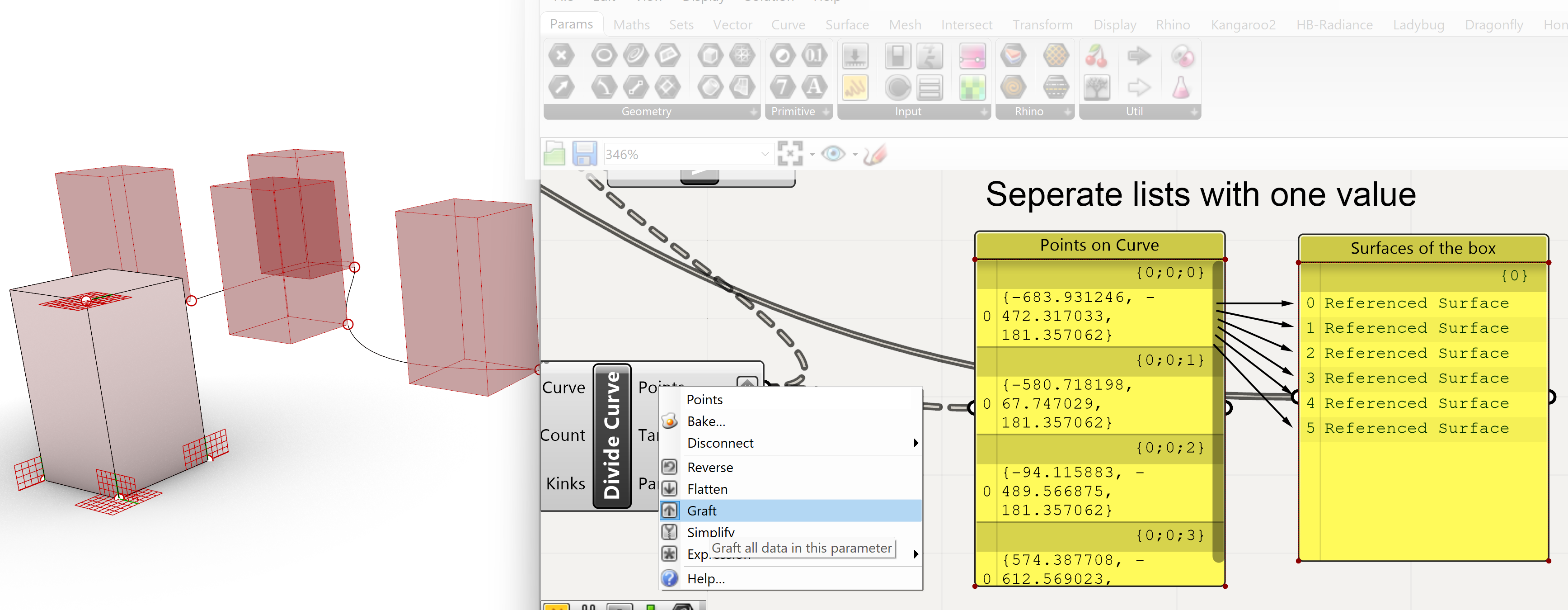
There is a simple solution for this misalignment of values. We can Graft the list. This option takes every value of the list and make a new list for each value. We know that if one of the list (point on curve list) has less values then the other list (Surfaces of the Box) the last value of first list will interact with the remaining values of the other list. That means that if we have one point on the curve, this point will interact with all the surfaces and therefore move the whole box to the point on the curve.
That means that if we make lists of each value of the points on the curve, the value of the list will interact with all the surfaces on the other list. Similar to the movement with one point. Because we have multiple lists this action is repeated for each single point on curve value.
To Graft the list ( converting each value in a separate list) we right click on the Point output of the Divide Curve component, and select Graft.
Example use: extracting in various ways target points from geometry
Displacement and alignment from plane to plane (orient option)
For the explanation we going to use previous setup. We have a box consisting of 6 surfaces which we are going to move to a surface. In this case we don’t only move the box , but we also want to orient it perpendicular to the surface.
A frame is a like a x and y grid located and perpendicular aligned to an surface. The fact that the frame is perpendicular to the surface means that if we can match that alignment with the frame of another object, the object will be placed perpendicular on the surface.
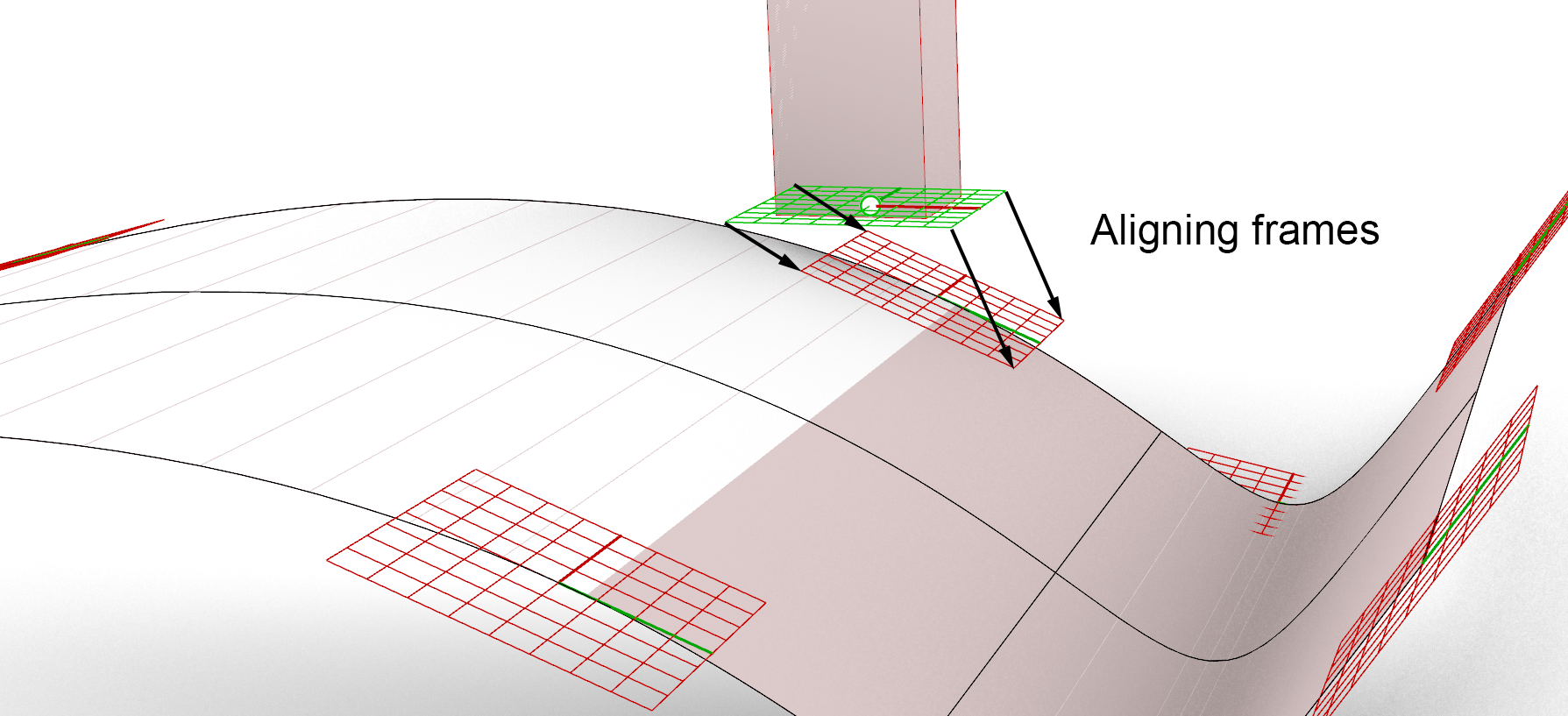
We create a double curved surface in Rhino and connect it to Grasshopper with the Surface parameter. To get the box aligned with the surface we need to extract a frame from the surface. The component Surface Frames lets us extract frames from the surface. Connect the Surface output of the parameter with the Surface input of the Surface Frames component. The U and V count can be altered with number sliders.
Parameter>> Geometry>> Surface parameter
Surface>>Utility>> Surface Frames
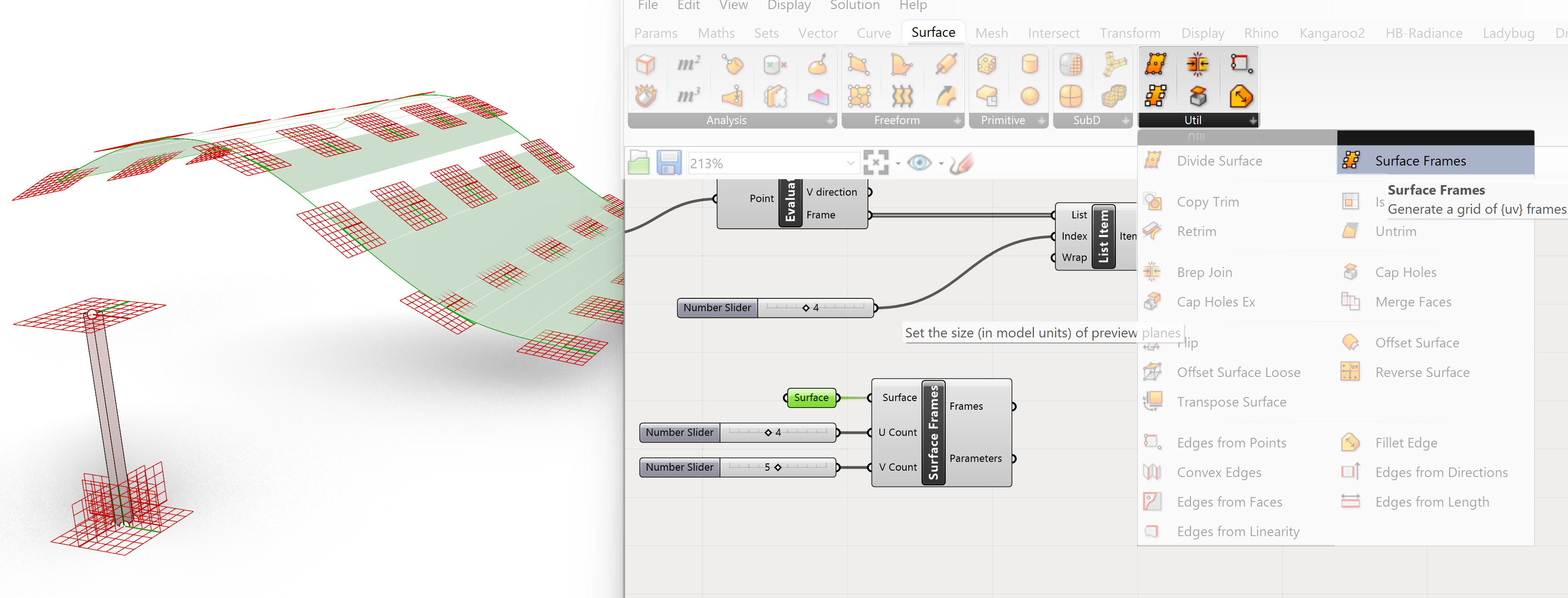
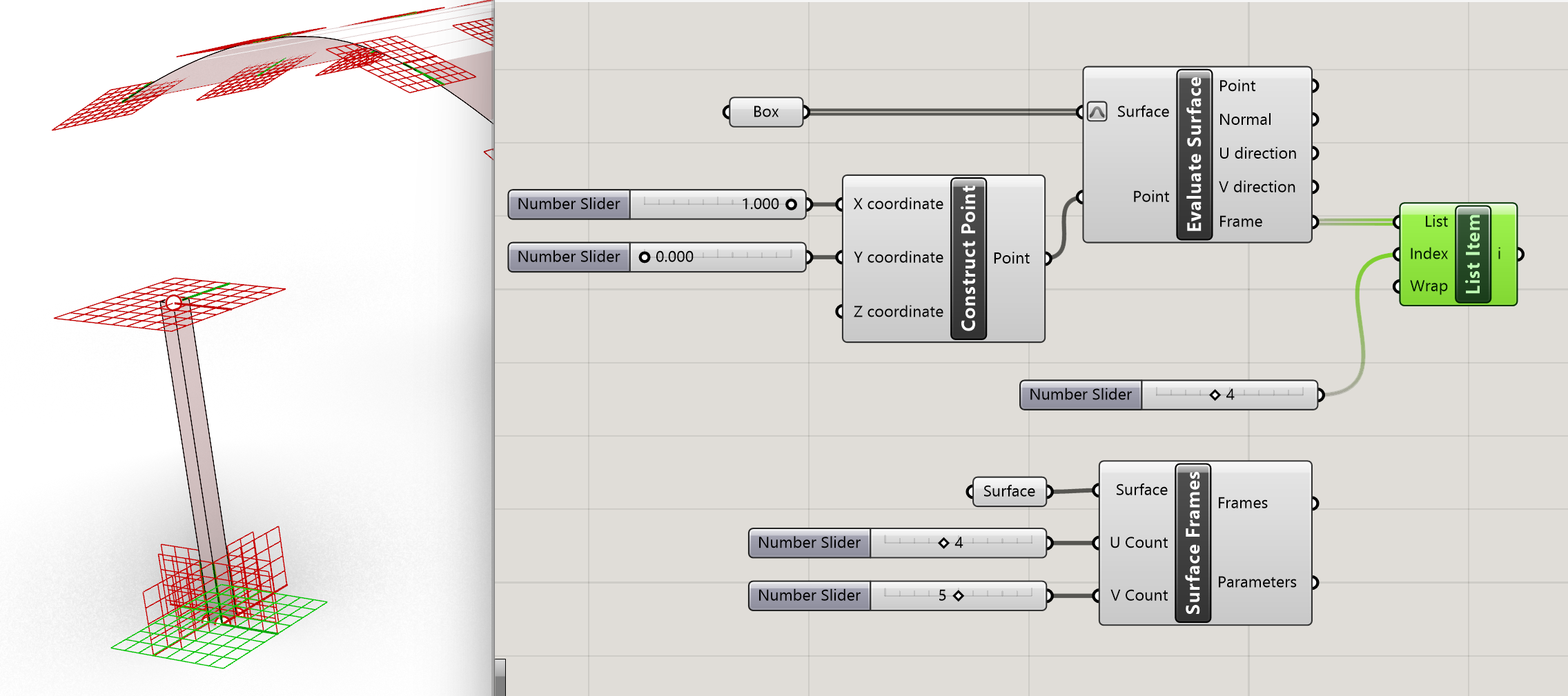
To extract a frame from the Box is simple because we already have a frame output from the Evaluate Surface component. Because we have multiple surfaces we need to select a single plane for the Orient action. We use the List Item to select the correct frame. Use a number slider to select the correct index of the frame. ( simple trick is to select the List Item component and move the slider to see which frame becomes green)
Sets>>List>>List Item
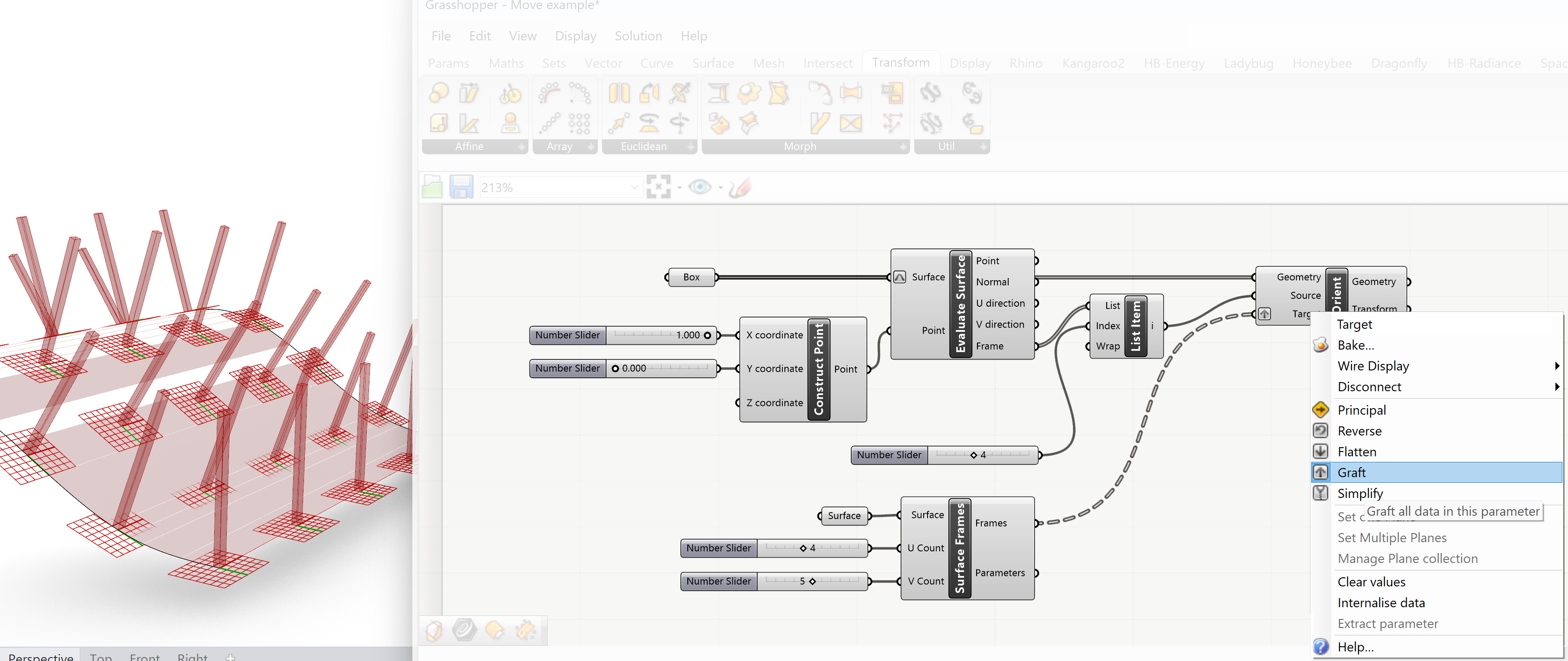
In this case we are not going to use the Move component but the Orient option. The Box output is connected to the Geometry input of the Orient component. The selected Frame of the box is connected to the Source of the Orient component. And the Surface frames output is connected to the Target input of the Orient component. You will have to Graft the Target input of the Orient component to make sure that all the 6 surfaces of the box will be correctly moved.
Transformation>>Euclidian>>Orient option
Transformations in Grasshopper 2/4
Rotatelink copied
There are a range of options of rotating geometry. The reason why there are several options has to do with the setup of the rotation axis or plane. For each situation one might be more suitable then the other options based on the geometry which has to rotated.
Rotate
To rotate geometry go to:
Transform>>Euclidean>>Rotate.
The Rotate component has 3 inputs.
- Geometry – the geometry which has to rotated
- The Angle – The standard value is defined in Radians, to change it to an angle in degrees input right click on the Angle input and select Degrees from the option list.
- Plane – The plane is a custom grid with an X and Y axis. The plane will define the rotational plane and the center of the Plane the origin of the rotation.
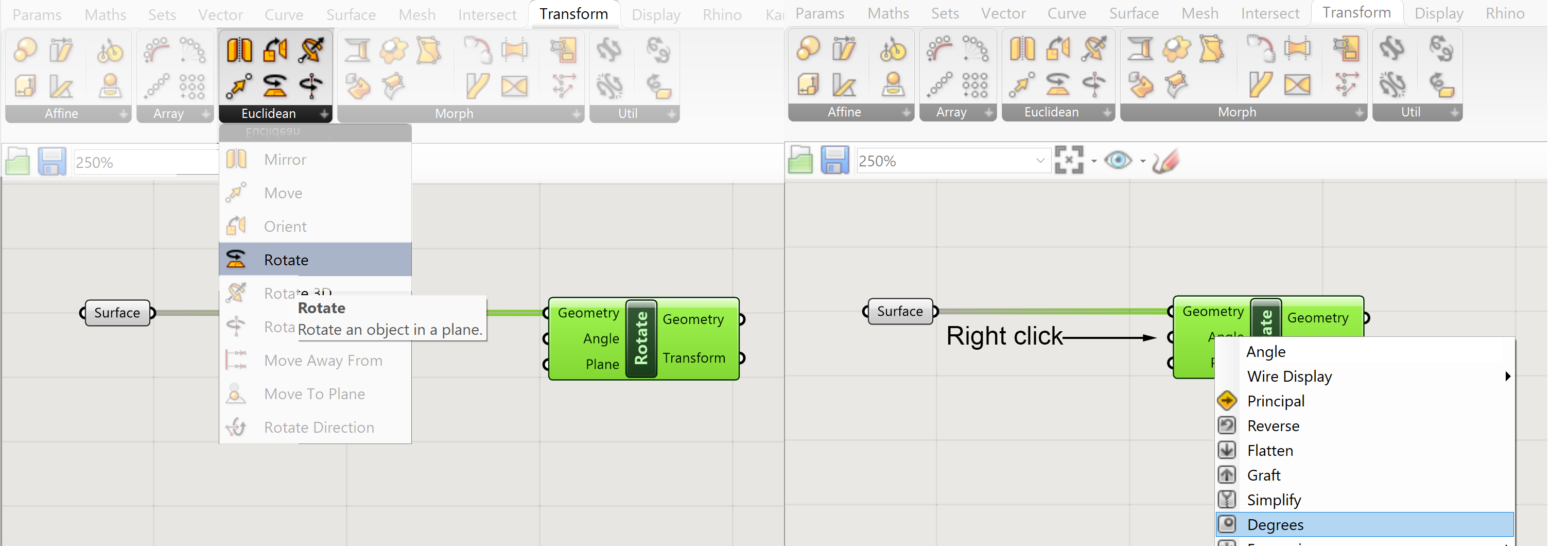
The geometry we have, the angle can be defined by a number slider. What is needed is to define a plane separate from the geometry or to extract a plane from the geometry. In this example we will rotate a box.
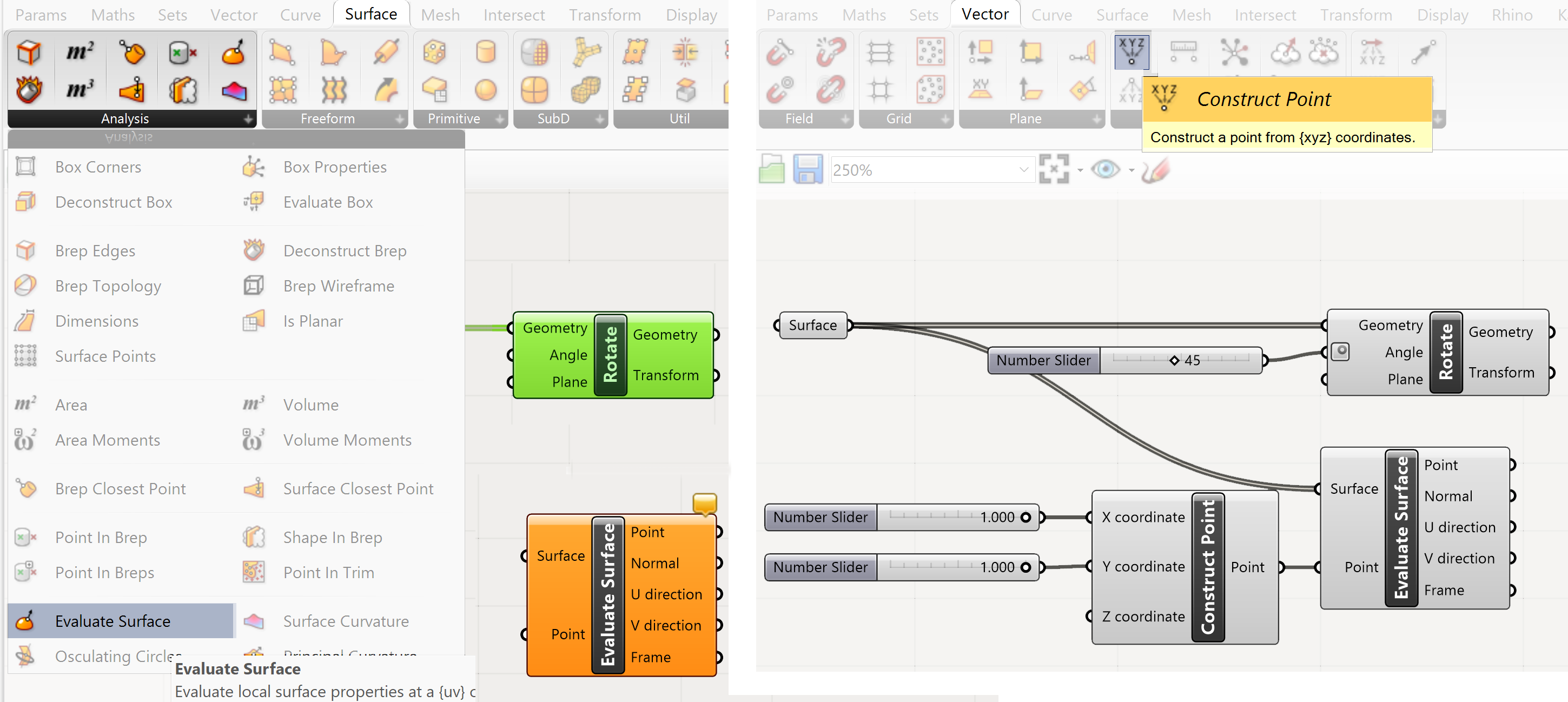
Extract a plane: There are several options for extracting a Plane. In this case we will follow the method discussed in the Move section of this tutorial. The box consists of 6 surfaces. These are connected to a Surface parameter.
With Evaluate Surface we can extract a Frame from each surface( Frame=Plane on geometry ) This is not the simplest option for a rotation setup but the most flexible.
The Point input of the Evaluate Surface component will be connected to a Construct point component defining the location of the plane on the surface.
Parameter>>Geometry>>Surface
Surface>>Analysis>>Evaluate Surface
Vector>>Point>>Construct point
In this case we reparametrize the input of the Geometry to so the length and width values of the surfaces are both set to 1, which forces the coordinate system on the surfaces to values between 0 and 1. This makes the input of the Construct Point component simpler.
- Connect number sliders with a max value of 1 to the Construct Point component. This will define the location of the Frame on the surface.
- Connect the Surface parameter to the Surface input of the Evaluate Surface component. Right click on the Surface input of the Evaluate Surface component and select reparametrize from the options list.
- Connect the Construct Point component to the Point input of the Evaluate Surface component.
Ther frame output of the Evaluate Surface component will have 6 frames defined, 1 for each of the 6 surfaces. With List Item we can select an appropriate frame.
Sets>>List>>List Item
Tip: select the list Item component to highlight the selected frame in green.
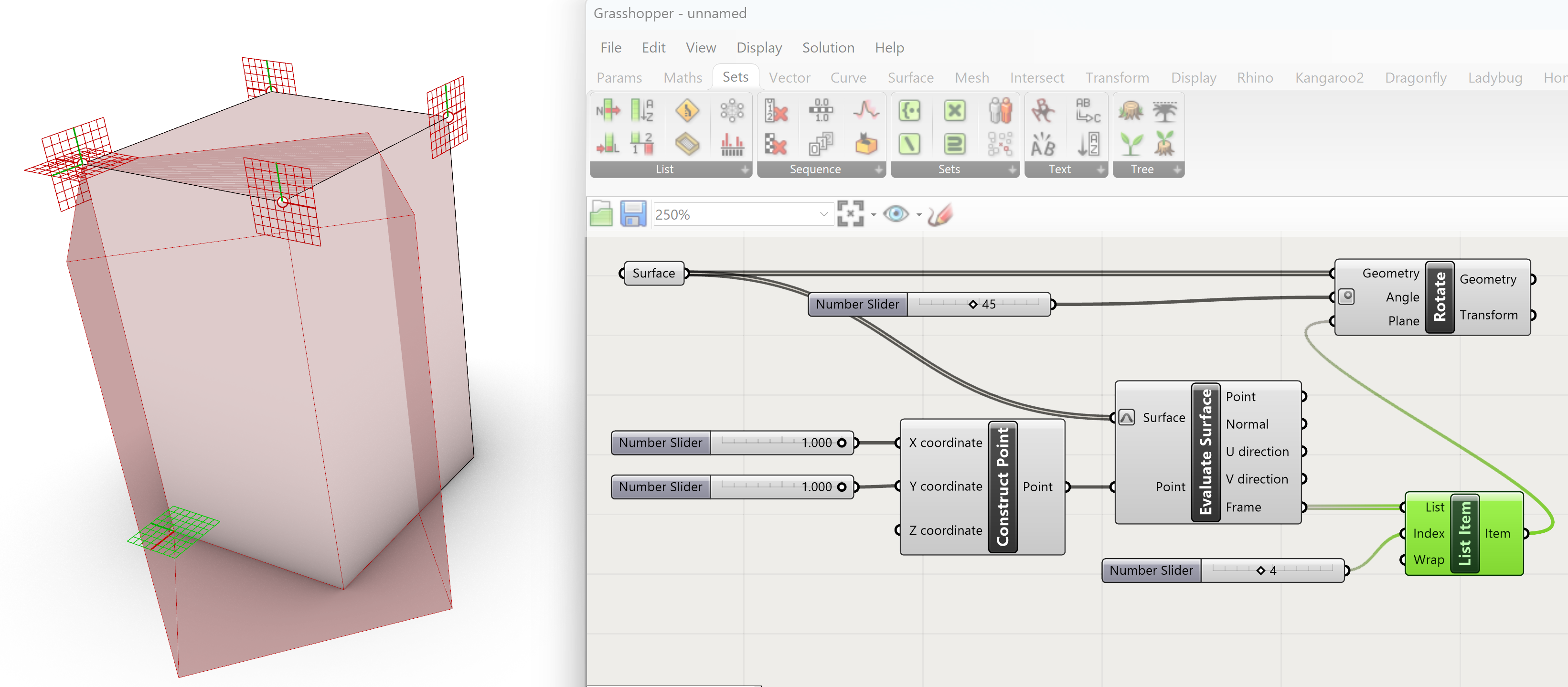
This network allows to change the selected frame by the List Item component, The location of that frame on the surface by the Construct Point component and the angle of the rotation by the number slider of the angle input of the Rotate component.
There are other options such as rotate 3D and rotate axis.
Rotate 3D:
Go to:
Transform>> Euclidian>> Rotate 3D
There are 4 inputs.
- Geometry
- Angle ( Right click on this input and select Degrees from the option list)
- Center , this is a point where the rotation is anchored around
- Axis , this is the rotational axis.
For this example we are going to use a solid box shape made in Rhino. This solid box can be connected to Grasshopper by a Brep parameter.
Parameter>>Geometry>>Brep
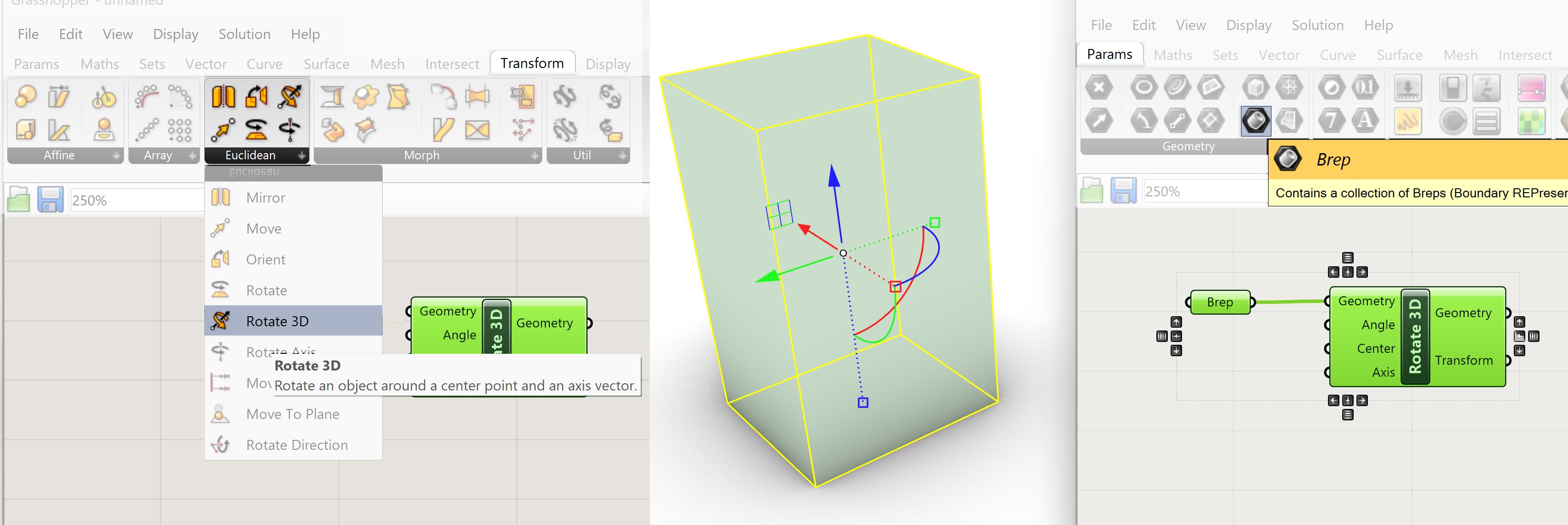
We connect a number slider to the Angle input of the Rotate 3D component (right click on the Angle input to select Degrees in the option list)
The Center is a point input. This can be:
- A single point defined in Rhino
- A set of points from for example a divided curve or surface.
- Or a point extracted from the geometry.
In this case we extract a point from the geometry. For extracting information from a Surface or Curve we can use the Analysis tab.
Deconstruct Brep this will give us the corner points of the box. The Vertices output will provide these points.
Surface>>Analysis>>Deconstruct Brep
Connecting a List Item to the Vertices output of the Deconstruct Brep component allows us to select the correct corner point of the box. It also gives us the edges of the box. Connecting a SList Item to the Edges output of the Deconstruct Brep component allows us to select the correct edge to be used as rotational axis from the box.
Sets>>List>>List Item
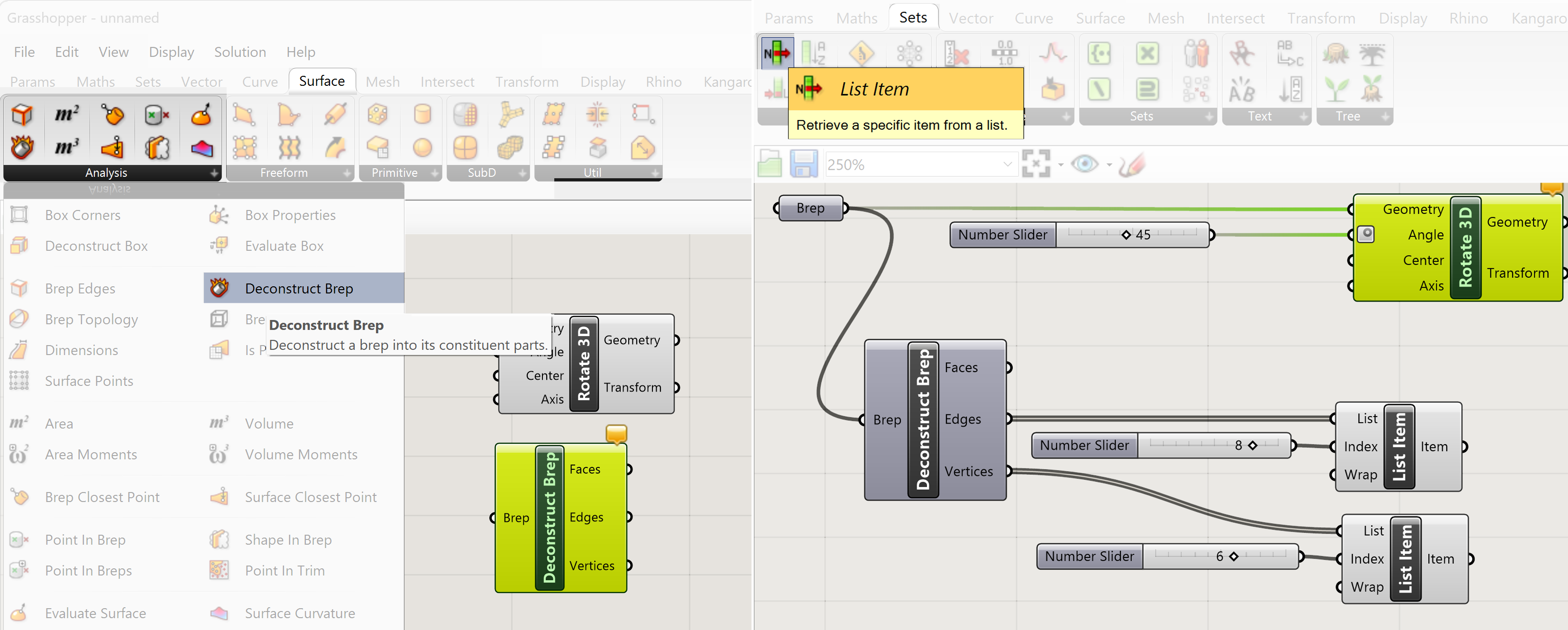
With the selection of the Edges and Vertices the List Items can be connected to respectively Center and Axis. The variables are in this case the Angle, the selected corner point as Center of rotation and the selected edge of the box as Rotational axis
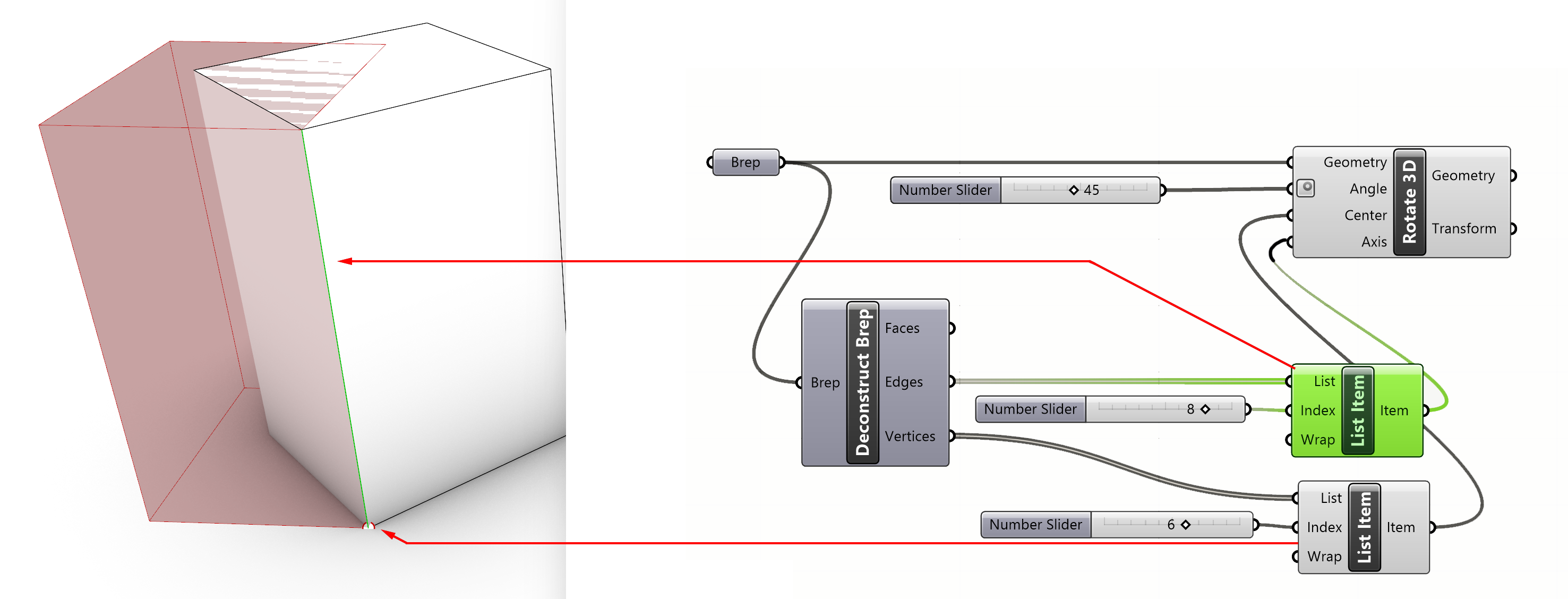
Rotate Axis
The Rotate Axis options is an option with a straight forward setup.
Transform >> Euclidean >> Rotate.
The input is:
- Geometry
- Angle
- Axis
That means that previous example also can be made with this option. In this case we can replace the anchor point of the rotational axis and the rotational axis by the location of a single axis. This is a simpler setup but also less flexible in use.
We are going to use a surface for the Geometry input of the Rotate Axis component.
For the Angle input of the Rotate Axis component we are going to use a Number slider. Also in this example we right click on the Angle input and select Degrees from the option list. So our input will be calculated as Degrees and not Radians.
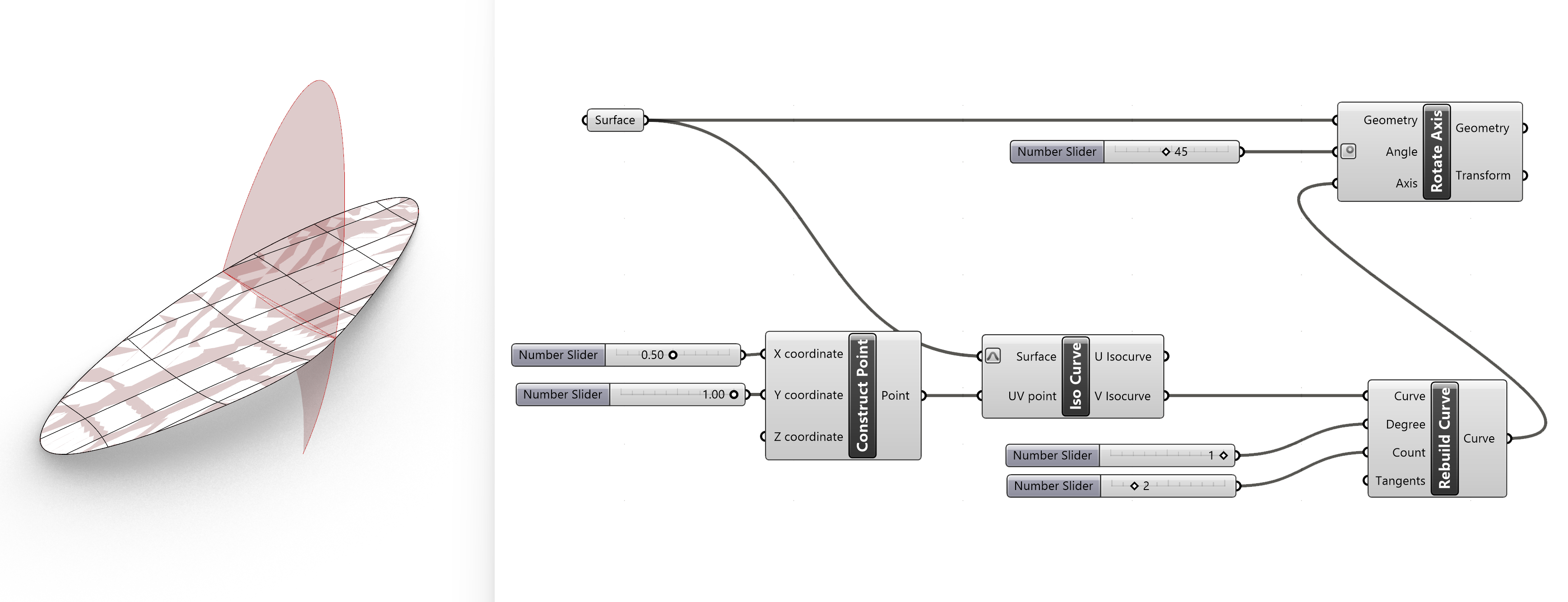
For the Axis input of the Rotate Axis component we can use any appropriate straight line, that can be an edge of for example a box or the edge of a rectangular plane. In this case however we going to use a curved surface with a curved edge.
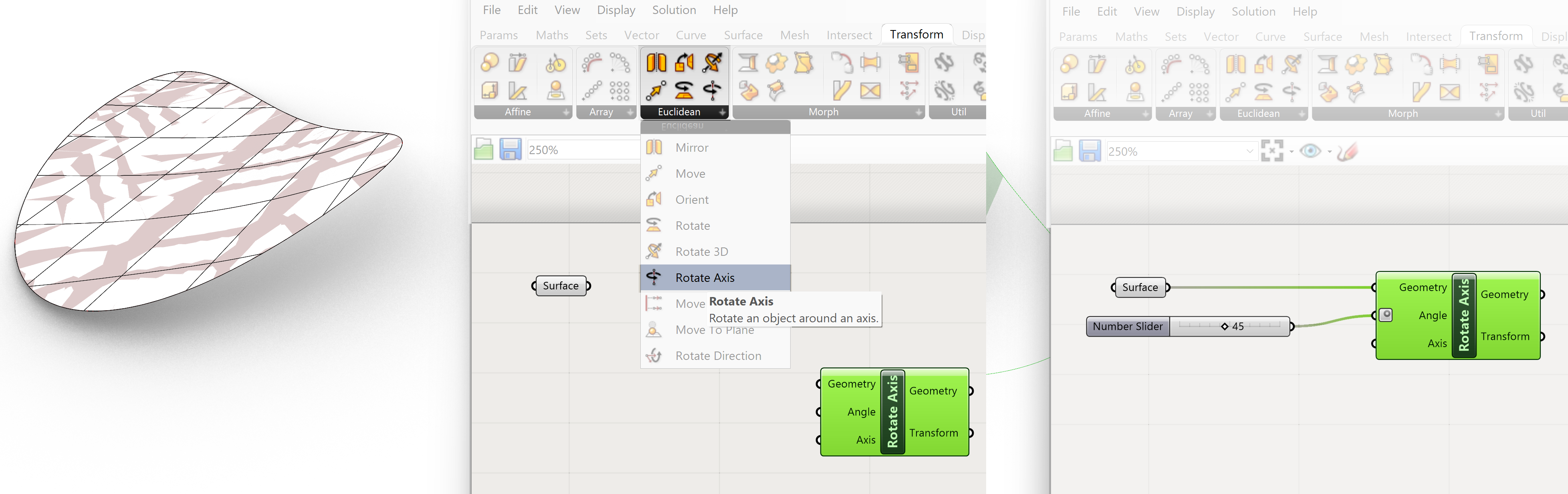
Because the edges are curved we can’t use them as a rotational axis. However we can extract a curve from the surface. These curves are called isocurves and represent a curve with one of the coordinates being constant and the other coordinate going from minimal to maximum coordinate value. The curves following the UV coordinates on the surface, the lines you see on a surface are iso curves. The line however can be curved so we apply a trick by selecting rebuilding the curve into a straight line.
To extract an Iso curve we go to Iso Curve :
Curve>>Spline>>Iso Curve
The Iso Curve component has 3 inputs
- Surface We right click on the Surface input and select Reparametrize from the option list. This will force the coordinates of the surface to values between 0 and 1.
- UV point We can use a Vector>>Points>>Construct Point component to define the U and V coordinates of the Iso Curve
The Construct Point component is connected to two number sliders with a max value of 1 due to the reparametrizing .
Vector>>Points>>Construct Point
The output of the Iso curve component is a curve in the U or V direction on the surface. Again the sliders can move this line up and down the surface. Problem however is that this curve is not a straight line. Therefore we will rebuild the curve to generate a straight line.
Go to rebuild the curve
Curve>>Utility>>Rebuild Curve.
The input of the Rebuild Curve are for:
- Degree input is 1 ( a 1 degree curve is always a straight line)
- Count input is 2 ( Two point to make up the line)
This output of the Rebuild Curve component will be connected to the Axis input of the Rotate axis component.
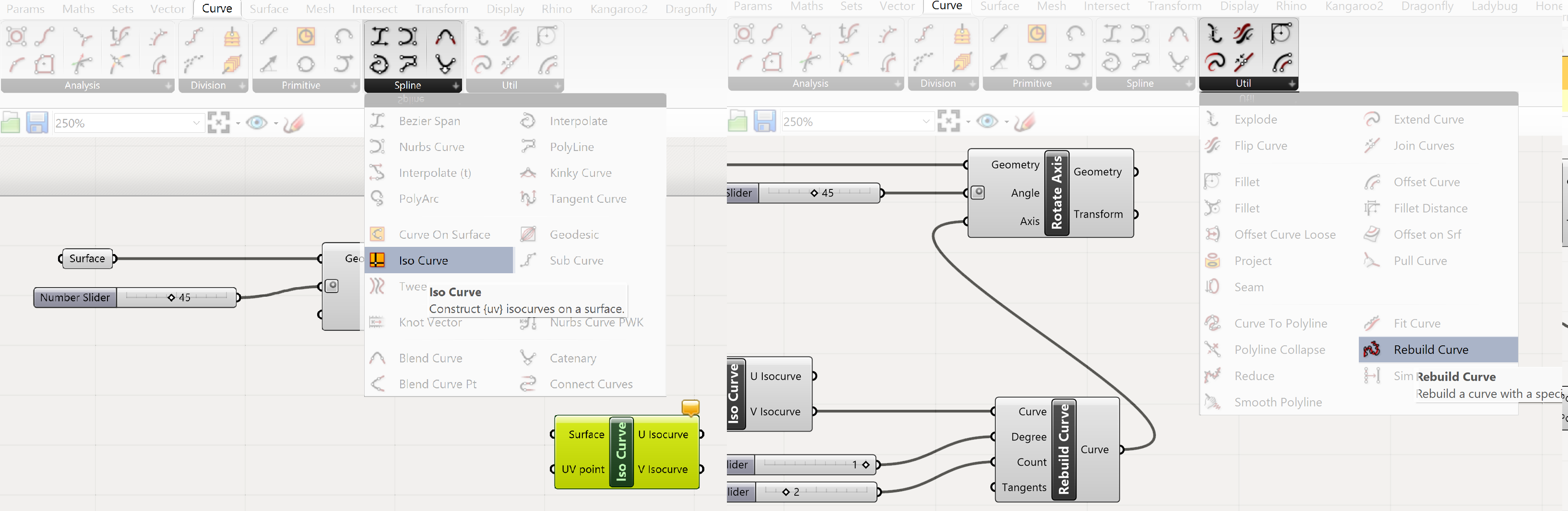
This example is different from the other examples because we extract an Iso Curve from a surface and straighten the curve so it can be used as a rotational axis. Off course if you have any geometry with straight edges, you can use these also. This example is to show that whatever geometry you have you can extract information from the geometry to build a rotational Axis.
Transformations in Grasshopper 3/4
Scalelink copied
Previous examples where more complex due to support the maximum freedom in applying the move and rotation options. For the Scale opotion we will go for the most simple options. With the knowledge gained from the previous explaination you should be able to enhance the capability of the scale options.
Uniform scale
To uniform scale an object we select the Scale component.
Transform>>Affine>>Scale
The component has 3 inputs:
- Geometry – this will be the Box
- Center – we have to define a point for this
- Factor – scale amount
This makes it straight forward. We are going to extract a point from the box. This is box will be connected to Brep ( Boundary representation ). Right click on the Brep component and select Set One Brep from the option list. Select the box in Rhino. This takes care of the Geometry input.
Parameter>>Geometry>> Brep
RMB >> Set one Brep >> select the box in Rhino
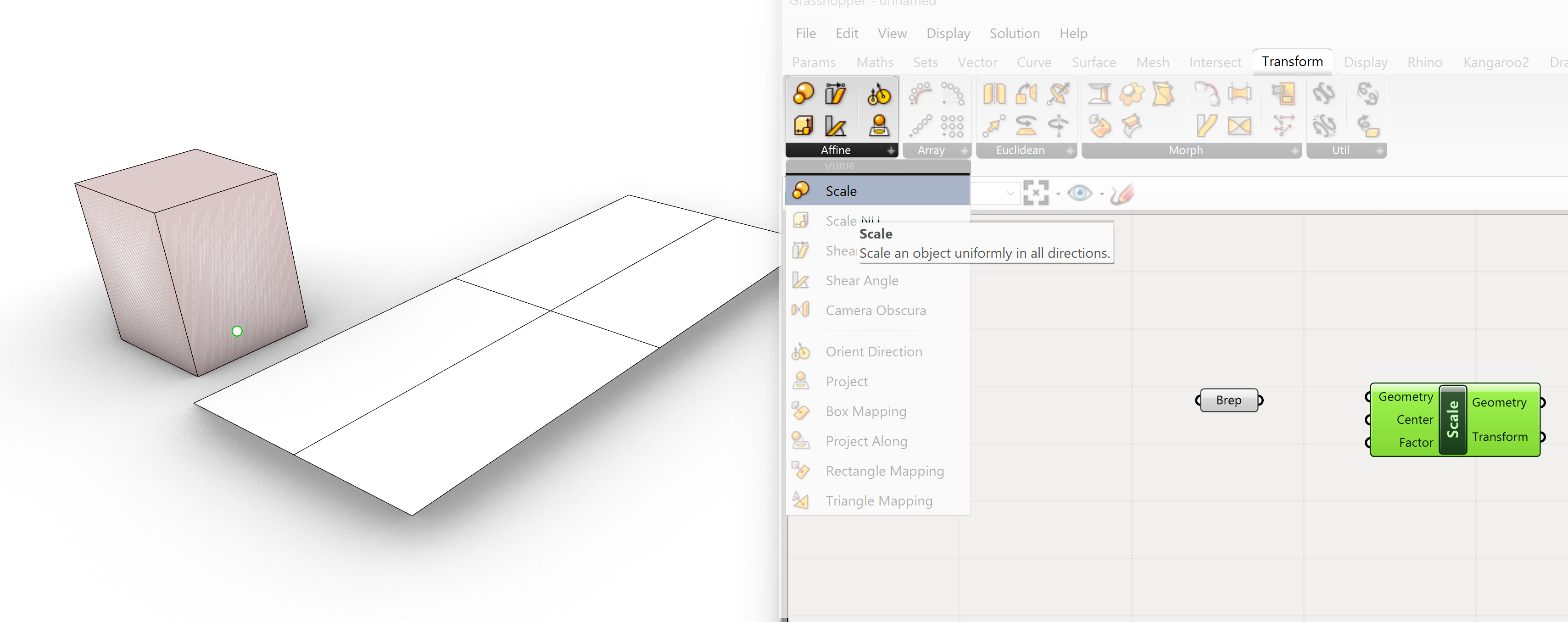
There are several options for extracting a point from the Brep. One simple option is to use an Evaluate Box component. The Box in this case is not the geometry but a Bounding Box. The Bounding Box is a close fitting box around an object. See it as a closely fitting cardboard box around an object. The object can be any shape, the bounding box is always box shaped. Because the object is also a box the Bounding Box will be exactly the same shape.
Surface>>Analysis>> Evaluate Box
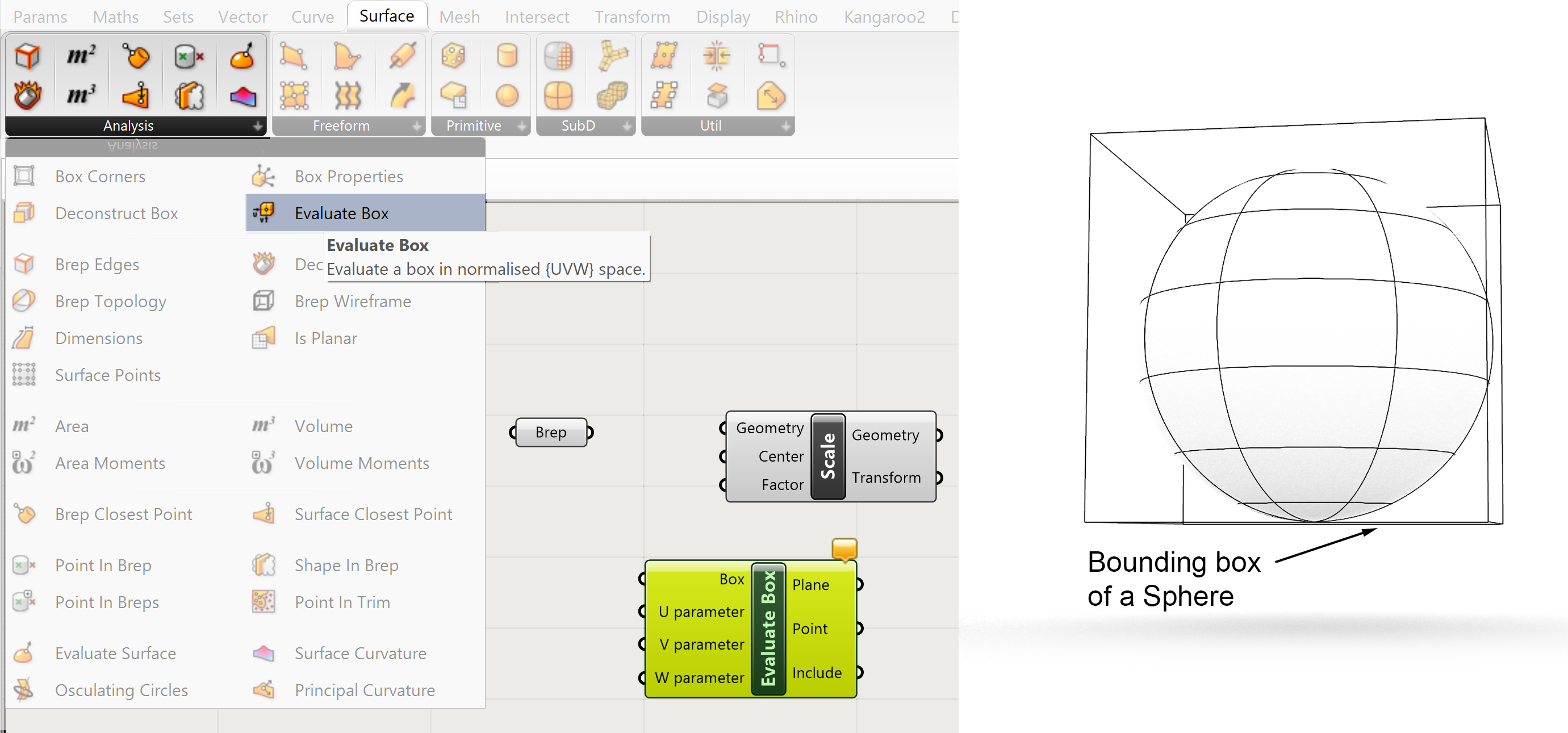
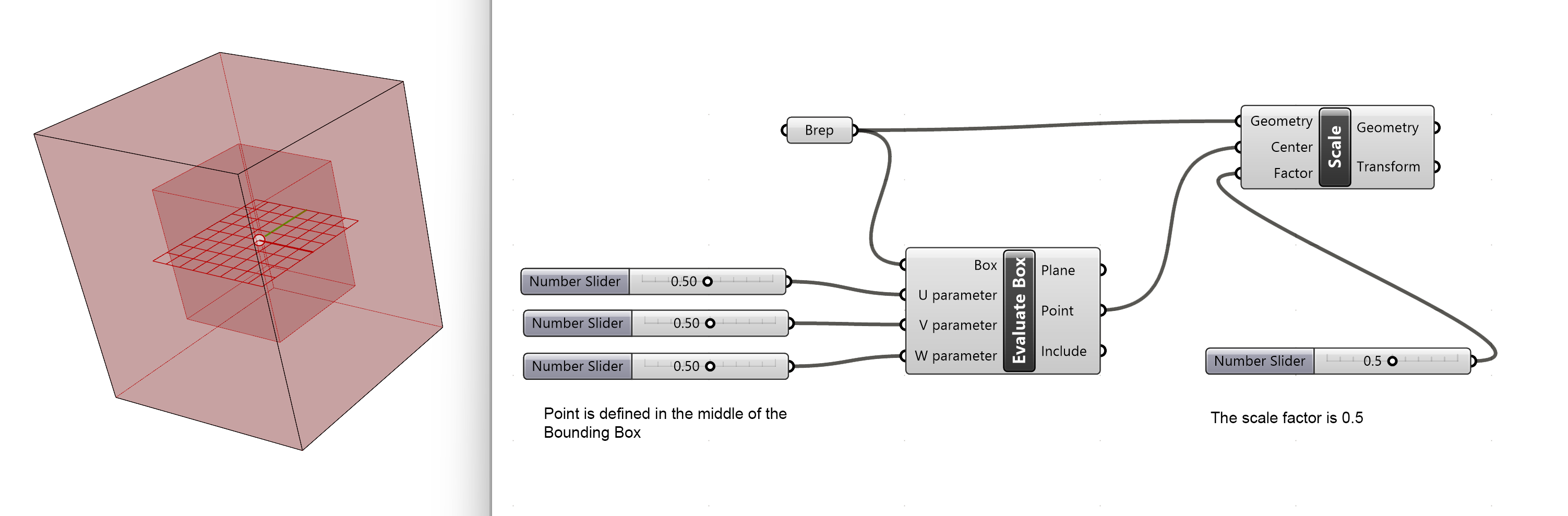
The Evaluate Box option has the advantage that you can define any location for the point anywhere within the Bounding Box by using U,V and W coordinates.
- We connect the Brep to the Box input. This creats the Bounding Box of the Brep
- We connect sliders to the U, V and W parameters to locate the point within the bounding box space. We will set the value to 0.5 for all the inputs. This will locate the point in the middle of the Bounding Box.
- The factor is set to 0.5 with a numberslider
Non-Uniform scale
Non Uniform scale allows to scale in 1 direction. This option will be explained with the same box we used in previous example.
To use the Non Uniform Scale option go to:
Transform>>Affine>> Scale NU
We can see that the Scale NU component has 5 inputs:
- Geometry – this is the object which has to be scaled. In this case the box – The Box is connected to a Parameter>> Geometry>>Brep parameter.
- Plane – We can extract a plane from the Brep by the Surface>>Analysis>>Evaluate Box component.
- X,Y and Z scale factor for the value we can use a numberslider
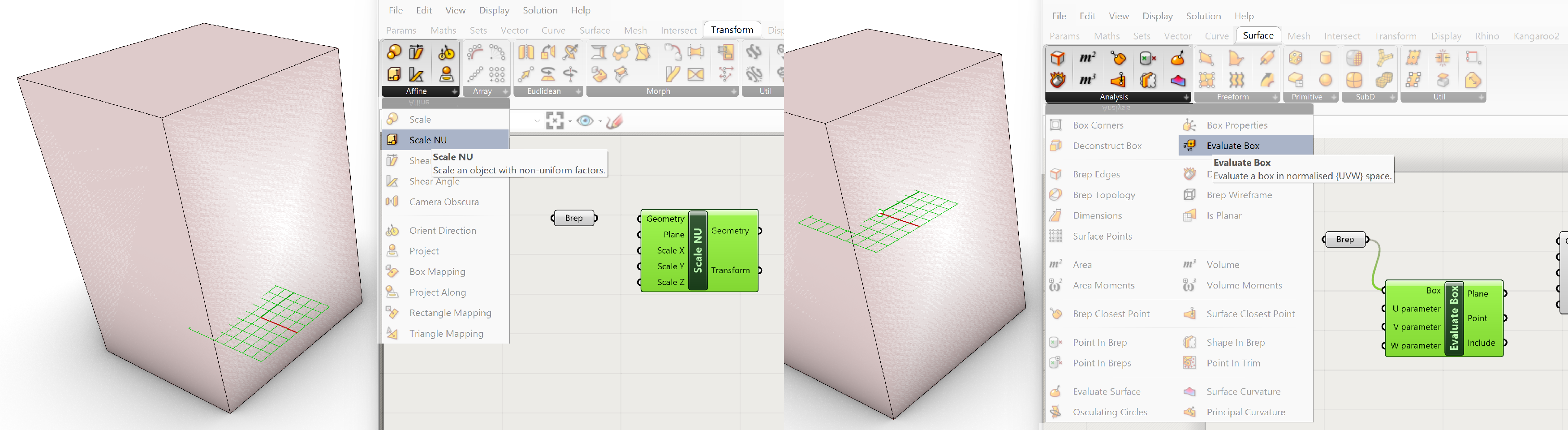
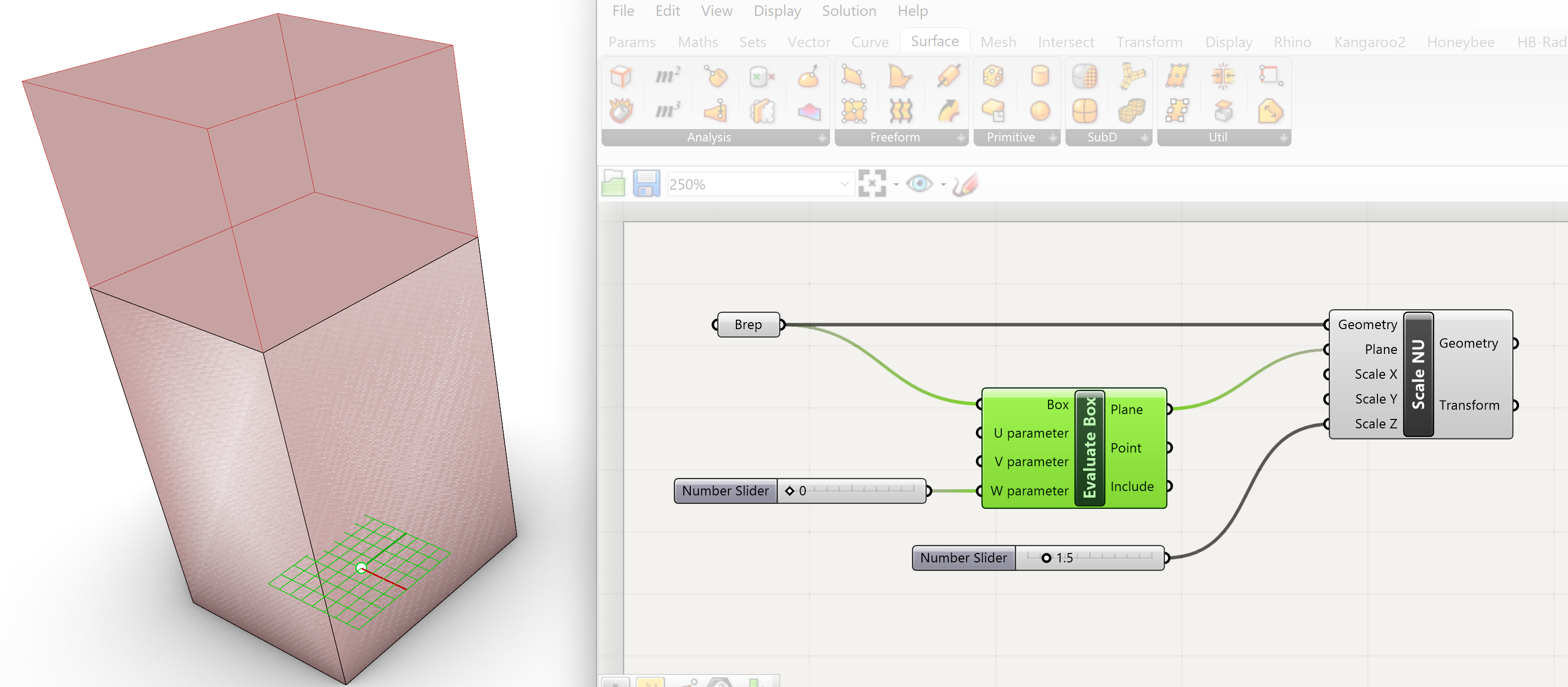
We move the plane of the Bounding Box to the bottom of the box by changing the W input to 0. The Scale NU setup can now be finished.
- We connect the Brep parameter to the Geometry input.
- The Plane output of the Evaluate Box component with the Plane input of the Scale NU component
- We couple a number slider to the W parameter.
Transformations in Grasshopper 4/4
Conclusionlink copied
xxx
Example file
You can download the example file on how to move and rotate here.
Write your feedback.
Write your feedback on "Transformations in Grasshopper"".
If you're providing a specific feedback to a part of the chapter, mention which part (text, image, or video) that you have specific feedback for."Thank your for your feedback.
Your feedback has been submitted successfully and is now awaiting review. We appreciate your input and will ensure it aligns with our guidelines before it’s published.
