Support Vector Machines (SVM)
-
Intro
-
Overview
-
Linear Kernel
-
Non-linear Kernels
-
Conclusions
Information
| Primary software used | Jupyter Notebook |
| Course | Computational Intelligence for Integrated Design |
| Primary subject | AI & ML |
| Secondary subject | Machine Learning |
| Last updated | November 19, 2024 |
| Keywords |
Responsible
| Teachers | |
| Faculty |
Support Vector Machines (SVM) 0/4
Support Vector Machines (SVM)
Support Vector Machines (SVM) are a type of supervised machine learning algorithm used for classification and regression tasks. They work by finding the optimal hyperplane that best separates data points of different classes in a high-dimensional space, maximizing the margin between them.
For this tutorial you need to have installed Python, Jupyter notebooks, and some common libraries including Scikit Learn. Please see the following tutorial for more information.
Exercise File
You can download the notebook version here:
Support Vector Machines (SVM) 1/4
Overviewlink copied

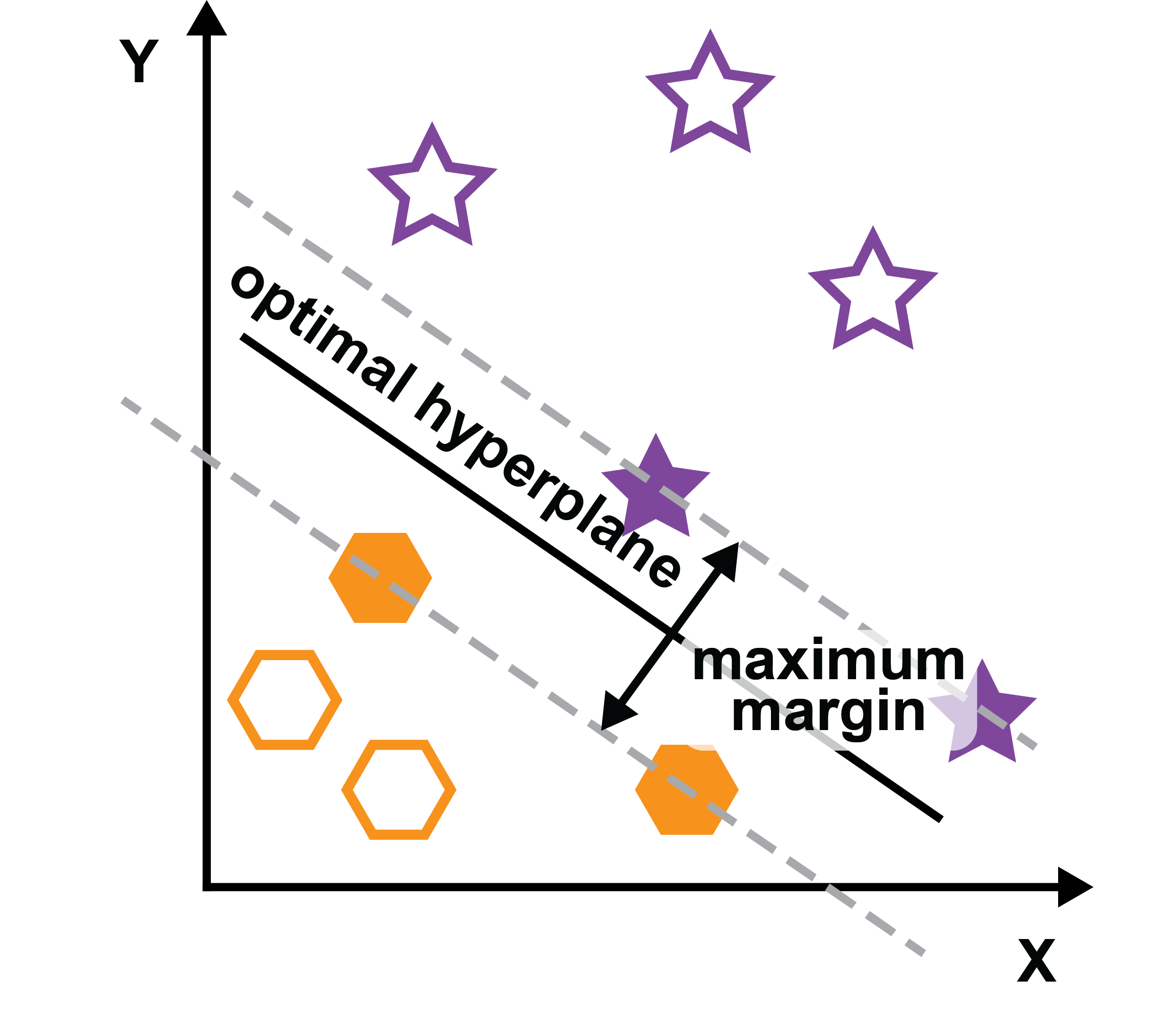
When determining the decision boundary to separate datapoints that belong to two classes, multiple decision boundaries can be found that correctly classify the samples. A decision boundary that falls equally between the separation in the data has the least risk of causing an error. Support Vector Machines determine the margin between the decision boundary and the nearest datapoint of both classes and then optimizes the boundary to be equidistant away from sample of both classes.
Although SVM by default uses a linear model and therefore linearly classifies data, the kernel trick can be used for non-linear classification. By using the Radial Basis Function (RBF), polynomial function, or sigmoid function, the data are mapped to a higher dimensional space which allows their non-linear separation.
Support Vector Machines (SVM) 2/4
Linear Kernellink copied

#Import scikit-learn dataset library
from sklearn import datasets
#Load dataset
wine = datasets.load_wine()
Print dataset information to understand the data.
# print the names of the features
print("Features: ", wine.feature_names)
# print the label classes
print("Labels: ", wine.target_names)
The output is:
Features: ['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
Labels: ['class_0' 'class_1' 'class_2']# print data(feature)shape
wine.data.shape
# print the (top 5 records)
print(wine.data[0:5])
# print the class labels
print(wine.target)
See the jupyter notebook for the output of these print statements
# Plot the records here
data_0 = np.array([w[0] for w in zip(wine.data[:,[0,1]], wine.target) if w[1] == 0])
data_1 = np.array([w[0] for w in zip(wine.data[:,[0,1]], wine.target) if w[1] == 1])
data_2 = np.array([w[0] for w in zip(wine.data[:,[0,1]], wine.target) if w[1] == 2])
plt.scatter(data_0[:, 0], data_0[:, 1], s=10, c='r', label = "Class 0")
plt.scatter(data_1[:, 0], data_1[:, 1], s=10, c='b', label = "Class 1")
plt.scatter(data_2[:, 0], data_2[:, 1], s=10, c='g', label = "Class 2")
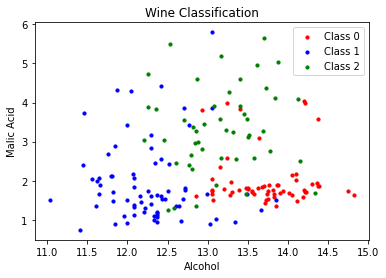
plt.title('Wine Classification')
plt.xlabel('Alcohol')
plt.ylabel('Malic Acid')
plt.legend()
plt.show()
SVM Kernels
SVM uses a kernel to determine the separation between the data. A kernel takes data as input and transforms it to create a more optimal decision boundary. Kernels can be linear or non-linear. Above, we used a linear kernel. SciKit Learn shows plots of three common SVM kernels: linear, polynomial, and radial basis function (RBF).
Linear Kernel
A linear kernel finds a decision boundary that is linear to separate the data into classes. Start by normalizing and splitting the data. Then train the model, predict the test data, and check the accuracy.
# Import required functions
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(wine.data, wine.target, test_size=0.3,random_state=109) # 70% training and 30% test
# Make pipeline for normalizing data
pipe = make_pipeline(StandardScaler(), LogisticRegression())
pipe.fit(X_train, y_train) # apply scaling on training data
pipe.score(X_test, y_test) # apply scaling on testing data, without leaking training data.
0.9259259259259259#Import svm model
from sklearn import svm
#Create a svm Classifier
clf = svm.SVC(kernel='linear')
# Linear Kernel
#Train the model using the training sets
clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy: how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# Which classes are commonly misclassified?
print('Confusion Matrix')
print(metrics.confusion_matrix(y_test, y_pred, labels=None))
The output is:
Accuracy: 0.9259259259259259
Confusion Matrix
[[21 0 0]
[ 3 15 1]
[ 0 0 14]]It is not possible to plot a 13 dimensional graph, so to visualize the SVM decision boundary, we can train a new SVM model on just the first 2 features of the dataset and visualize the decision boundary in 2D.
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# Select 2 features / variable for the 2D plot that we are going to create.
X = wine.data[:, :2] # we only take the first two features.
y = wine.target
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
model = svm.SVC(kernel='linear')
clf = model.fit(X, y)
fig, ax = plt.subplots()
# Set-up grid for plotting.
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlabel('Alcohol')
ax.set_ylabel('Malic Acid')
ax.set_title('Decision Surface of Linear SVM')
plt.show()

Support Vector Machines (SVM) 3/4
Non-linear Kernelslink copied
Some common non-linear kernels used for SVM include polynomial and radial basis function (RBF). You can find additional information about what kernels can be used on the SciKit Learn website
Start by normalizing the data. To normalize data, it is best to use a pipeline because this first scales the training data and then applies the same scale to the test data without leading any training data.
# Import required functions
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(wine.data, wine.target, test_size=0.3,random_state=109) # 70% training and 30% test
# Make pipeline for normalizing data
pipe = make_pipeline(StandardScaler(), LogisticRegression())
pipe.fit(X_train, y_train) # apply scaling on training data
pipe.score(X_test, y_test) # apply scaling on testing data, without leaking training data
The output is:
0.9259259259259259Radial Basis Function (RBF) Kernel
SVM has a parameter called C which can be adjusted to allow for a certain level of mis-classification to have a more optimized location of the decision boundary. When using the RBF kernel, there is another parameter, gamma, which can be adjusted to change how linear the boundary is. From Scikit-learn Plot RBF Parameters: “The gamma parameter defines how far the influence of a single training example reaches, with low values meaning ‘far’ and high values meaning ‘close’. To find the best gamma and C values for RBF, it is a good idea to do an initial search. For this initial search, it is possible to use a logarithmic grid with basis 10.
from sklearn.svm import SVC
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV
C_range = np.logspace(-2, 10, 13)
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X_train, y_train)
print("The best parameters are", grid.best_params_, "with a score of", grid.best_score_)
The output is:
The best parameters are {'C': 100000.0, 'gamma': 1e-07} with a score of 0.944Train the model based on the gamma and C values that were determined above.
#Import svm model
from sklearn import svm
#Create a svm Classifier
clf = svm.SVC(kernel="rbf", gamma=1e-07, C=100000.0) # RBF Kernel
#Train the model using the training sets
clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy: how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# Which classes are commonly misclassified?
print('Confusion Matrix')
print(metrics.confusion_matrix(y_test, y_pred, labels=None))
The output is:
Accuracy: 0.8703703703703703
Confusion Matrix
[[19 2 0]
[ 4 15 0]
[ 0 1 13]]
We can again visualize the decision boundary on the first 2 features of the dataset. It will take a few more seconds to run as it processes the data.
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# Select 2 features / variable for the 2D plot that we are going to create.
X = wine.data[:, :2] # we only take the first two features.
y = wine.target
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
model = svm.SVC(kernel='rbf', gamma=1e-07, C=100000.0)
clf = model.fit(X, y)
fig, ax = plt.subplots()
# create a mesh to plot in
h = .02 # step size in the mesh
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, edgecolors='k')
plt.xlabel('Alcohol')
plt.ylabel('Malic Acid')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.title("Decision Surface of SVM using RBF Kernel")
plt.show()
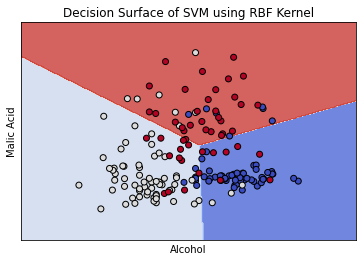
The graph to the side shows how the optimal parameters using the RBF kernel created an almost linear separation between the data. If we increase the gamma value, the separation boundary creates curves around specific groups of points. See this in the example below. For the sample dataset, this is less accurate. Additionally, higher gamma values can lead to overfitting.
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# Select 2 features / variable for the 2D plot that we are going to create.
X = wine.data[:, :2]
# we only take the first two features.
y = wine.target
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
model = svm.SVC(kernel='rbf', gamma=5, C=100000.0)
clf = model.fit(X, y)
fig, ax = plt.subplots()
# create a mesh to plot in
h = .02 # step size in the mesh
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) # Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, edgecolors='k')
plt.xlabel('Alcohol')
plt.ylabel('Malic Acid')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.title("Decision Surface of SVM using RBF Kernel")
plt.show()

TASK: Plot a validation curve for the gamma value through SciKit Learn to see how the value of gamma impacts the accuracy of the model.
Polynomial kernel
The polynomial kernel has three parameters: degree, gamma, and C. The most common degree used is either 2 or 3 because larger degrees are more likely to overfit. Gamma can be set to “auto” which means it uses 1 / n_features. C is the same as the C used for the RBF kernel.
#Import svm model
from sklearn import svm
#Create a svm Classifier
clf = svm.SVC(kernel="poly", degree=2, gamma="auto", C=100000.0) # Polynomial Kernel
#Train the model using the training sets
clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy: how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# Which classes are commonly misclassified?
print('Confusion Matrix')
print(metrics.confusion_matrix(y_test, y_pred, labels=None))
The output is:
Accuracy: 0.9259259259259259
Confusion Matrix
[[21 0 0]
[ 2 16 1]
[ 1 0 13]]from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# Select 2 features / variable for the 2D plot that we are going to create.
X = wine.data[:, :2] # we only take the first two features.
y = wine.target
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
model = svm.SVC(kernel='rbf')
clf = model.fit(X, y)
fig, ax = plt.subplots()
# Set-up grid for plotting.
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlabel('Alcohol')
ax.set_ylabel('Malic Acid')
ax.set_title('Decision Surface of SVM with Polynomial Kernel')
plt.show()
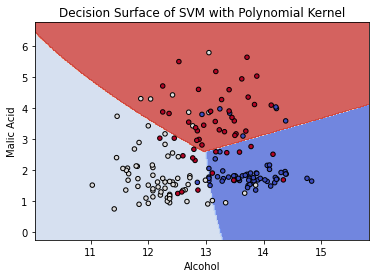
TASK: Plot a validation curve for the degree value through SciKit Learn to see how the number of degrees impacts the accuracy of the model.
Support Vector Machines (SVM) 4/4
Conclusionslink copied
- SVM optimizes the decision boundary so that it falls equally between the separation in the data because it has the least risk of causing an error
- Although SVM uses a linear model, the kernel trick can be used to map the data to a higher dimensional space and then non-linearly classify it
- Plotting two features with the decision boundary can help visualize how SVM is working
- Some common non-linear kernels used for SVM include polynomial and radial basis function (RBF)
- Non-linear kernels have parameters which need to be adjusted to get the best result, and the more we increase nonlinearity the more increase overfitting risk
Write your feedback.
Write your feedback on "Support Vector Machines (SVM)"".
If you're providing a specific feedback to a part of the chapter, mention which part (text, image, or video) that you have specific feedback for."Thank your for your feedback.
Your feedback has been submitted successfully and is now awaiting review. We appreciate your input and will ensure it aligns with our guidelines before it’s published.
