Computational Methods for Design and Research
-
Intro
-
Background
-
Parametric Design and Parametric Modelling
-
The Importance of the Parameterisation Process
-
Performance Based Design, Performance Assessment and Simulations
-
The Importance of Simulation Choices
-
Optimization and Optioneering
-
Design Exploration Through Optimization
Information
| Last updated | November 27, 2024 |
| Primary category | |
| Secondary category |
Responsible
| Faculty |
Computational Methods for Design and Research 0/7
Computational Methods for Design and Research
This is an overview of definitions and explanation of computational methods for design and research.
The following definitions and explanations refer to the context of geometric models, performance simulations and optimization in Computational Design and related research areas. They are functional to the tutorials included in DigiPedia but should not be considered exhaustive. For thorough and comprehensive overviews about parametric modelling, performance simulations and optimization please refer to the scientific literature. If you are following the TU Delft ABE BSc courses BKB2WV3 and / or BKB3WV4, the definitions contained in this document are relevant for your studies.
Computational Methods for Design and Research 1/7
Backgroundlink copied
Following the definition proposed in Caetano et al. (2020), we refer to Digital Design as a design process in which the computer is used, we refer to Computational Design as a design process in which computational methods, techniques and tools are used to develop design solutions. Therefore, using digital tools for drafting and visualising design options should be considered an instance of Digital Design rather than computational design. Computational design entails the emergence of new design approaches related to the use of computational methods, techniques and tools. Parametric design and related techniques of parametric modelling allow to generate and evaluate design options and are an instance of computational design.
Parametric Modelling is the process of representing a design form through parametrized components and attributes (Barrios, 2005; Turrin et al., 2011). Parametric modelling uses associations to construct geometric objects with editable attributes. Attributes can be expressed by independent values, which act as input to the model. Attributes can be expressed by fix values or by variables. A variable parametrized attribute, also known as a design variable, enables the parametric model to produce different design forms. The relationship between design variables and output geometry is defined by a hierarchical chain of dependencies established during the initial parameterization process. Within this hierarchy, certain geometric attributes function as independent variables, while others are dependent. The associations between different attributes in a parametric model enable the generation of forms that maintain all pre-established relationships among geometric entities. These solutions are referred to as instances of the parametric model.
Parametric modelling is widely used in architectural design to integrate engineering considerations, especially when handling complex geometries and exploring alternative design options. It naturally integrates with building performance simulation, enabling the generation and evaluation of design options in a continuous workflow. By combining parametric modelling with performance assessment techniques (such as computational performance simulation), it is also possible to automate the search for optimal solutions by using optimisation algorithms. This document discusses the generation, evaluation, and optimisation of design solutions through various computational methods.
These computational techniques can be used to support design as well as research processes. If you are interested in an overview with examples for design and for research, you may watch this 30-minute video:

References
- C. Barrios (2005). Transformations on Parametric Design Models, in: Computer Aided Architectural Design Futures. Springer, Netherlands. pp. 393–400
- Turrin, M., Von Buelow, P., & Stouffs, R. (2011). Design explorations of performance driven geometry in architectural design using parametric modeling and genetic algorithms. Advanced Engineering Informatics, 25(4), 656-675.
- Caetano, I., Santos, L., & Leitão, A. (2020). Computational design in architecture: Defining parametric, generative, and algorithmic design. Frontiers of Architectural Research, 9(2), 287-300.
Computational Methods for Design and Research 2/7
Parametric Design and Parametric Modellinglink copied
Parametric Design
According to Barrios (2005), parametric design is the process of designing with parametric models or in a parametric modelling setting. Caetano et al. (2020) refers to parametric design as a design process that uses parameters and rules to structure an algorithmic thinking. Focusing on geometry for design, parametric modelling is the process of making a geometric representation of a design with components and attributes that have been parameterized, meaning they are expressed by means of parameters. But what is a parameter?
Parameter
According to the Oxford Dictionary, a parameter is “A numerical or other measurable factor forming one of a set that defines a system or sets the conditions of its operation”; mathematically, a parameter is “A quantity whose value is selected for the particular circumstances and in relation to which other variable quantities may be expressed”. According to the Merriam-Webster Dictionary, a parameter is “An arbitrary constant whose value characterizes a member of a system (such as a family of curves)”. For example, a certain value for the radius of a circle defines a certain circle; but a radius can have different values, in which case different circles are defined. Therefore, a parametric model for design uses values that characterize certain configurations and are different for different configurations; and in relation to which other variable quantities may be expressed. What does this mean pragmatically?
Parametric Model
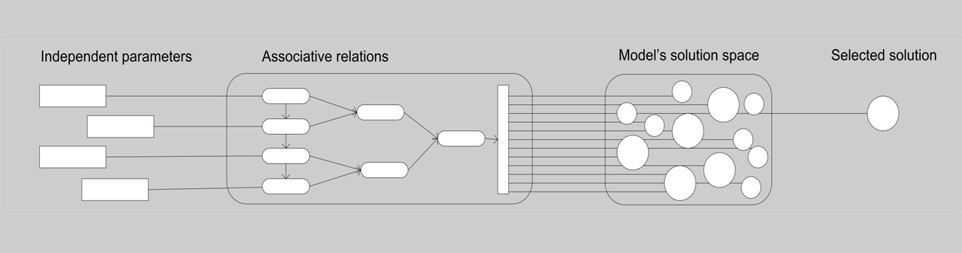
For definition, parametric modelling has the capability to represent both geometric entities and their relationships, based on the so-called associative geometry. This means that through the digital model a network of dependencies is described among geometric entities. Geometric entities can be single entities or features, intended as objects in which various entities are already assembled. The relationships among entities or features are structured in a hierarchical chain of dependencies. Some attributes are described by independent values (independent parameters) and others by values that vary in relation to other attributes. When varying these, the independent parameters act like inputs to the model and the dependent attributes are processed by receiving data from their related attributes. This flow of data keeps the network of dependencies consistent, which itself remains constant, but processes the input values by generating variations of the output. These variations are produced as different solutions of the model. A parametric model can be seen as a family of models as big as the possible combinations of independent values, therefore sometime even infinite.
Parameterisation Process
Before building a parametric model, the designer defines which components of the model vary and how the variation occurs. This parameterization process determines the attributes subject to parametric transformations and the rules governing these transformations. It includes deciding the independent parameters and design variables and the associative relations. Usually, the result of a parameterization process is a (hierarchical) structure, which describes the dependency chain established in the model, starting from the independent parameters.
Parametric Structure of a Model
Sometimes it is indicated as a “graph” or “dependency chain”. The dependency chain of a parametric model is a hierarchical structure that organizes how data flow from inputs to outputs. In a large
majority of parametric modelers, the way in which data flows from the inputs to generate the outputs is based on single-directional graph parsing, which means that a graph of geometric entities and relations is parsed entity by entity from the independent parameters to the geometric outputs (Coenders, 2011).
Note: most of current software for parametric design provides a thorough visualisation of the dependency chain, from input variables to the final geometry, passing through a visualisation of the process as a graph.
Parametric Solution Space
Once the parametric model is built, a solution space is obtained. When a parametric model is built in design process, the solution space of a parametric model may represent (part of) the design space. (The notion of design space versus solution space of a parametric model is an important concept not addressed here but worth deepening in your future reading.) The solution space of a parametric model consists of all the possible design options that can be generated by varying the independent variables of the model. Each design option is also called an instance of the model. As Barrios (2005) points out, each instance represents a unique set of transformations based on the values assigned to the variables. Different independent variables and hierarchical associations (in other words, different outputs of the parameterization process) produce different solution spaces.
Examples of Related Software
While systems with this potential are well known in the engineering field, they have become commonly used in the architectural field more recently. Examples are Revit with Dynamo (Autodesk), Catia (Dassault Systèmes), SolidWorks (Dassault Systèmes), Generative Components, named GC, in Microstation (Bentley) and Grasshopper, named GH, which is a plug-in for Rhinoceros (McNeel & Associates). As Aish and Hanna (2017) highlight, most parametric design environments offer multiple representations. In addition to the geometric representation, parametric modelling software for architecture include also a visual graph-based data flow representation, and sometimes a text based program representation.
Useful Sources
Do you want to know more? For a broader overview of parametric modelling types:
- Janssen, P., & Stouffs, R. (2015, May). Types of parametric modelling. In Proceedings of the 20th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA) (pp. 157-166).
References
- C. Barrios (2005). Transformations on Parametric Design Models, in: Computer Aided Architectural Design Futures. Springer, Netherlands. pp. 393–400
- Turrin, M. (2013). Performance Assessment Strategies: A computational framework for conceptual design of large roofs. Tu Delft.
- Coenders, J., (2011), Networked Design: next generation infrastructure for computational design, Ph.D. Delft University of Technology
- Aish, R., & Hanna, S. (2017). Comparative evaluation of parametric design systems for teaching design computation. Design Studies, 52, 144-172.
Computational Methods for Design and Research 3/7
The Importance of the Parameterisation Processlink copied
This section addresses the importance of the parameterisation process when developing a parametric model for design or research in the built environment. (Note: If you are following the BKWV3 course in the TU Delft ABE BSc program, you are studying parametric design and the potentials of generating design alternatives can be applies in design processes to explore alternative design options. If you are following the BKWV4 course in the TU Delft ABE BSc program, you are studying parametric modelling in research and the potentials of generating design alternatives in research processes to investigate the effect of certain parameters.)
The first key step in parametric modelling is the parameterization process. This regards the very early phase of the process, because a parametrization process takes place to build a parametric model. A parametric model is quite goal oriented. The first question is always “why are we building a parametric model?”.
Parametric modelling has several possible applications. Here we focus on automatically generating design alternatives which allows a designer to quickly visualise design options and possibly find unexpected geometric configurations, emerging from the high number of possible variable recombination. Parametric modelling allows a designer to rapidly assess the effect of design choices, through parametric control, on qualitative design aspects and aesthetic criteria. Parametric modelling is also useful for performance-driven design applications: A designer can analyse the design options produced with a parametric model through building performance simulation software to search for design options responding to one or multiple design performance criteria.
The use of parametric modelling to automatically generate design alternatives finds application also in research processes to investigate the effect of certain parameters in the built environment.
Building a parametric model without specifying the objective of the design exploration or research investigation is pointless. The identification and analysis of the design exploration objectives should always occur before the parameterization process begins. An inappropriate parameterization process can compromise the utility of a parametric model. In fact, the parametrization process affects the boundaries of the solution space (Turrin, 2013) and the quality of the design options contained therein. Specifying the design requirements at the outset of the parametrization process helps identify design parameters that are relevant to the problem at hand and is therefore essential to limit the search process to valid design alternatives. In other words, a design variable should affect a geometric aspect of a design solution, which in turn will affect a design performance.
For instance, if we are looking for a design solution that allows for a certain amount of daylight in the rooms, building a parametric model to explore the effect of various indoor doors sizes would be useless. If instead, we are investigating daylight in indoor spaces, we might build a parametric model to explore the effect of various window sizes and positions on indoor daylight. Furthermore, we might want to include indoor doors’ sizes variations within our model, to investigate, for example, indoor connectivity or evacuation time in case of emergency.
Sometimes the identification of design attributes that affect a building performance criterion is straightforward. In the example above, window size is directly related to the amount of daylight entering a room. In such cases, the parametrization process is immediate: one can use window width and height as independent variables. In other cases, identifying design attributes that affect performance criteria is very difficult. For example, when investigating the effects of walls on the acoustic behaviour of a space, the relationship between geometry and performance is not that obvious. To understand which variables, or independent parameters, should be included in the model, one should run preliminary tests to study the problem. Several methods serve to increase the awareness of the designer (or researcher) concerning the relationship between geometry and performance during or before the parametrization process. This includes preliminary explorations via physical models, performance analysis and simulations among others.
In summary, a parametrization process should be based on well-defined logic, a clear design strategy and solid motivations; and preliminary investigations may be required. Sometimes, this process is also iterative and building certain parametric models may reveal relationships between geometry and performance that were unknown to the designer. In these cases, revising the parametric model might be beneficial.
The time invested in the parametrization process is another aspect worth considering. Parameterization is a time-consuming process requiring a scientific approach: one must formulate hypotheses about which variables are relevant to the design problem and test them before finalising the model. Developing a model that embeds design considerations early on is important as the hierarchical chain of dependencies allows little flexibility in changes once a model has been created (Kilian, 2006). This means that a parametric model can rarely be adjusted without major changes in its graph structure.
References:
- Turrin, M. (2013). Performance Assessment Strategies: A computational framework for conceptual design of large roofs. Tu Delft.
- Kilian, A. (2006). Design innovation through constraint modeling. International journal of architectural computing, 4(1), 87-105.
Computational Methods for Design and Research 4/7
Performance Based Design, Performance Assessment and Simulationslink copied
In Computational Design, according to Caetano et al. (2020), performance-based design refers to a design process in which the designer sets a performance target, whereas an algorithm identifies design solutions that best meet the performance target. Performance-based design often relies on parametric modelling in combination with performance assessment (such as via simulations). The design alternatives generated with a parametric model can be assessed based on how well they respond to a certain performance criterion (or design requirement).
A parametric model can generate a potentially infinite number of alternative design solutions. Therefore, one must define a precise selection criterion to navigate the space of design possibilities and make choices. A common strategy involves analysing design options through building performance evaluations, including climatic comfort (thermal behaviour, daylight levels, etc.) and structural performance. Digital tools for building performance evaluations are already integrated with parametric design software. Parametric modellers also allow for the development of custom evaluation tools through dedicated text-based scripting environments.
The process of design exploration can be carried out by manually adjusting the parameters to iteratively search for design solutions with the highest performance. Alternatively, the generation, evaluation and search processes can be automated by dedicated algorithms.
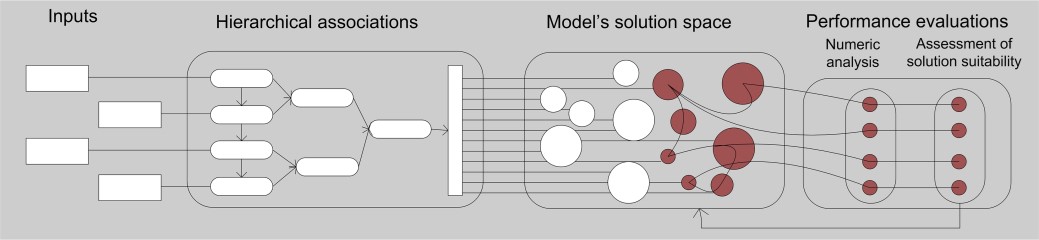
Performance evaluations are commonly used in the late design stages to validate and detail appropriate design solutions (Attia, 2018). However, these evaluations should also be performed at the early design stages, when the most crucial decisions are made (Sariyildiz, 2012).
This section introduces the concept of performance indicators and assessment in the context of computational simulations, focusing on techniques suitable for early design evaluations and research purposes.
Performance Indicators
A performance indicator is a measurable value used to assess the performance of something. In performance-based design, we consider a variety of building performance indicators to assess the performance of design options. Performance indicators allow you to check whether a design option meets certain performance requirements.
Suppose you are designing a building. To establish how a design alternative performs, one must first specify what the performance indicators are. While certain design criteria are not easily quantifiable, it is possible to identify performance requirements and define indicators for several building engineering tasks. For example: “having sufficient daylight in a room” can be translated into certain ranges of daylight indicators, such as daylight factor or amount of lux on the floor, daylight autonomy, etc.; “being thermally comfortable” can be translated into certain ranges of air temperature, mean radiant temperature, humidity, air-speed etc. or into thermal comfort models such as the Predicted Mean Vote, etc. Different performance indicators can be used for the same project.
The same applies in research. Suppose you are performing a research project to investigate how the form of office rooms impacts the daylight distribution on the office desks. To establish the impact of the form, you need to be able to quantify the daylight on the office desks. Also, in this case, you will most probably use performance indicator intended as measurable values.
Performance Simulations
Once the appropriate performance indicators are identified, in a design process, simulations can be used to quantify the values for each design option and identify the one with the highest performance. Similarly, in research they can be used to investigate performances. Various digital environments play a key role in simulation for building performance assessment.
According to the Oxford English Dictionary, simulating is “producing a computer model of something”; similarly, the Collins English Dictionary defines simulation as a “representation of a problem, situation, etc., in mathematical terms, especially using a computer”. The Cambridge English Dictionary defines simulation as “a model of a set of problems or events that can be used to teach someone how to do something, or the process of making such a model.” In addition to the purpose of assessment, the intention for learning is emphasized here as a crucial component in using simulations in design processes.
What examples of performance simulations can you think of? Daylight simulations, thermal simulations, and structural simulations are just a few of the possible examples.
The recognized value of assessing performance based on measurements and analyses led to an increased integration of performance simulations during the design process (Augenbroe, 1992; Lam et al., 2002). The adoption of simulations in the very early design phase is more recent. Nowadays, the importance of performance assessment using simulation in the early design process has been acknowledged by several scholars as well as practitioners. According to Mahdavi and Lam (1991), systematic “front -ended” studies based on digital simulations to aid preliminary design decisions should be preferred to the traditional approach, in which the role of building simulation is relegated to the “back-tail” of the design process. As Caldas and Norford (2002) point out, ‘by using simulation tools, it is possible to engage in a design practice based on feedback loops between making design decisions and evaluating their environmental impact, as a way to inform the ongoing process of design’. The value of simulations as a learning tool is also commonly acknowledged. In Simon (1996), simulations are described as a source of new knowledge: they help discover the consequences of premises, which may be impossible to uncover otherwise. Using simulations as a design aid, instead of as a confirmation tool, is at the core of performance-based design.
Additional Readings on building performance simulations
References
- Attia, S., Bilir, S., Safy, T., Struck, C., Loonen, R., & Goia, F. (2018). Current Trends and Future Challenges in the Performance Assessment of Adaptive Façade Systems. Energy and Buildings 179:165-182. doi: https://doi.org/10.1016/j.enbuild.2018.09.017
- Sariyildiz, IS. (2012). Performative computational design. In s.n. (Ed.), Proceedings of ICONARCH-I: International congress of architecture-I (pp. 313-344). Selcuk University.
Computational Methods for Design and Research 5/7
The Importance of Simulation Choiceslink copied
Simulations must be selected based on several aspects, including:
- What indicators need to be quantified;
- What inputs are needed in the simulation to estimate the values of these indicators;
- What is the computational cost of the simulation;
- What is the level of simulation detail required by the application. For instance, preliminary assessments can be rougher (as long as reliable), whereas final documentations need to be more detailed.
- And more.
Other sections of DigiPdedia address these matters more in depth.
Practical note:
Additionally, For the students using Rhino and GH, one important consideration also regards whether a simulation requires import-export from Rhino-GH or not. Simulations using geometric models exported from Rhino-GH and automatically imported into simulation software: When students work in GH for the parametric models, then they can link several simulation tools to GH. Some simulation tools are external to GH, and GH plug-ins allow for automatic import and export of files between external simulation software and GH. For example, this is the case for Geco – which used to connect GH and Ecotect (nowadays not really used anymore). Simulations using geometric models within Rhino-GH: Alternatively, there are several simulation tools available also directly within GH. Often, they recall external calculation engines on the backstage, but the user does not perceive it – as the entire interface is built in GH only. Examples are: DIVA for GH, simulating daylight; Honeybee; Ladybug; Karamba; etc.
Computational Methods for Design and Research 6/7
Optimization and Optioneeringlink copied
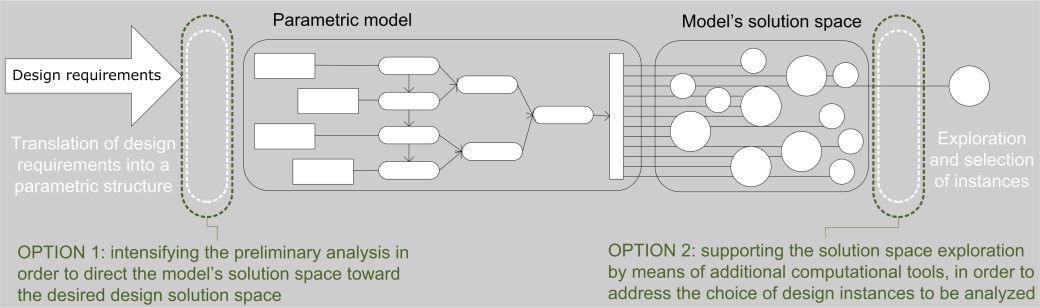
The combined use of parametric models and simulation tools allow generating and evaluating design options in a continuous pipeline. However, when the solution space is large, it is not possible to analyse every design option one by one. As illustrated in the image below, in some cases one can narrow down the search space through the selection of a few relevant variables. In others, the problem cannot be simplified, and the search process must be carried out by an automated procedure. In these cases, one of the options is to use optimization algorithms.
This section includes text revised from Turrin (2013) pages 307-310 and reflects on the use of optimisation to search across parametric solution spaces in architectural design.
Generally speaking, looking to support the search in large design solutions spaces, a possible scenario concerns the combination of an automated parametric generation of design alternatives and their performance evaluations with search algorithms to find the satisfying parametric configurations among the entire collection of instances of the parametric model (an exhaustive search). Even though it might provide satisfactory support in case of a relatively small number of independent parameters, this scenario would become impractical as soon as the parametric model is described by a relatively large set of independent variables. The reason for this is the ineffectiveness in terms of time and computational effort of a systematic generation and performance analysis of each instance, resulting in a much too cumbersome process even when automated. With respect to this, optimization algorithms which guide the generation of parametric design alternatives can be a preferred scenario, expected to provide more effective support.
In mathematics, optimization is the process of finding inputs to a function that minimize or maximize its value, where the inputs may be subjected to constraints (Pardalos and Resende, 2002). Optimization algorithms are among the computational procedures available for solving optimization problems (Baños et al, 2011). Optimisation algorithms differ in search technique, solution analysis method and implementation. The following section briefly overviews some of the algorithms commonly used in building design optimisation.
- Trajectory-based methods, such as simulated annealing and stochastic hill climbing, start the search process from a single design solution. This is iteratively adjusted to improve a performance metric. The output of this process is a unique solution.
- Population-based methods, like Genetic Algorithms, start the search process from a population of design solutions. The most performing design options are selected at each iteration, and their variables are recombined to produce a new population of even more performing solutions. The output of this process is a set of solutions, among which the designer usually selects the most performing one. (Baños et al, 2011).
Gradient-based methods are another class of algorithms starting from one design solution. These are based on mathematical procedures and converge fast. However, they are only effective when the relationship between design variables and performance – also called fitness function – is expressed by a continuous differentiable function.
Conversely, trajectory-based and population-based methods are stochastic, meaning they introduce a certain amount of randomness in the optimisation process. This helps the algorithm find valid solutions (not optimal in the absolute sense, but sub-optimal) even when the fitness function is non-differentiable (Renner and Ekart, 2003).
Although stochastic methods are generally preferrable, selecting an optimisation method should be performed on a case-by-case basis, as its effectiveness will depend on the nature of the design problem, the characteristics of the design space and the design constraints (Monks et al., 2000). Current software packages for design optimisation include many algorithms, allowing a designer to select the one that best fits the intended application.
The Case of Evolutionary Algorithms
This section includes text revised from Turrin (2013) pages 313-314 and describes using Evolutionary Algorithms in architectural design.
Evolutionary Algorithms (EAs) are a class of population-based methods widely used in design optimisation. For a comprehensive overview see Elbeltagi et al. (2005). According to Guliashki et al. (2009), the popularity of EAs is due to their ease of implementation, flexibility, robustness, and ability to find multiple optimal solutions for a wide range of problems. EAs, such as Genetic Algorithms (GAs), optimise design solutions by simulating the process of natural evolution.
For clarity, it should be noted that other algorithms use different principles from the natural behaviour, such as particle swarm and ant-colony systems. Examples include how ants find the shortest route to a source of food and how birds find their destination during migration. The behaviour of such species is guided by learning, adaptation, and evolution.
GAs operate on generations of large sets, or populations, of design solutions. They simulate the process of natural evolution by selecting design options based on their fitness (performance value) and recombining and mutating their genes (design variables) to create a new population of better-performing solutions at each generation (optimisation iteration). GAs can be used to optimise a design option for one or multiple criteria simultaneously. This method is widely applied in numerous fields in and beyond the design disciplines. Goldberg (1989) provides an exhaustive description of how GAs work.
Although GAs are among the most used optimization algorithms in architectural design, they are not necessarily the best option in all cases. Some scholars have highlighted the importance of considering alternatives (Wortmann, 2017).
For the sake of completeness, it should be mentioned that other algorithms, such as particle swarm and ant-colony, mimic biological systems to address design optimisation problems.
Genetic Algorithms (GAs)
The following terminology applies to GAs, but overlaps with many general concepts used in design optimisation:
- Design variables: are the variables defining the solution space; These are continuously updated during the optimization process (e.g. your sliders in GH if you use GH).
- Objectives: are the performance indicators minimized or maximized during the optimization process (e.g. a daylight factor to be maximized; the weight of the structure to be minimized; solar gain to be either minimized or maximized; etc.)
- Fitness function (Objective function): a fitness function represents the relationship between variables (design parameters) and performance (objective). It evaluates how well a given set of variables (or solution) performs relative to a defined objective.
- Single-objective optimization: this optimization targets one objective;
- Multi-objective optimization: this optimization involves optimising multiple objectives simultaneously.
- Pareto frontier: The set of all non-dominated solutions in a multi-objective optimization problem. A solution is considered non-dominated if improving its performance with respect to one objective would result in a trade-off, worsening its performance in at least one other objective.
- Mutation rate: Mutation is a GA operator that ensures diversity in the population of design solutions during the optimisation process. It works by altering one or more genes (design variables) defining a design solution. The mutation rate is a value between 0 and 1, representing the percentage of design solutions that will be mutated during each generation. This value affects the speed and effectiveness of the optimisation process. For example, setting a mutation rate of 0.9 affect 90 individuals for a population size of 100. The optimisation algorithm will require a large number of generations for converging, as any progress made in selecting more performing solutions will be counterbalanced by random design variable updates. On the other hand, setting 0.01 as a mutation rate will only affect one design solution per generation. In this case, the optimization algorithm can converge too quickly to a sub-optimal solution.
- Population size: the number of individuals (design solutions) produced for each generation.
- Crossover probability: A number between 0 and 1 representing the percentage of design solutions that will be recombined after each generation. During recombination, variable values (genes) from two parent solutions are exchanged to produce two new offspring solutions.
Additional Readings on Evolutionary Algorithms
- Machairas, V., Tsangrassoulis, A., & Axarli, K. (2014). Algorithms for optimization of building design: A review. Renewable and Sustainable Energy Reviews, 31, 101-112. https://www.sciencedirect.com/science/article/pii/S1364032113007855
- Wortmann, T., Waibel, C., Nannicini, G., Evins, R., Schroepfer, T., & Carmeliet, J. (2017). Are genetic algorithms really the best choice for building energy optimization. In Symposium on Simulation for Architecture & Urban Design (SimAUD) https://www.researchgate.net/profile/Thomas_Wortmann/publication/317277483_Are_Genetic_Algorithms_really_the_best_choice_for_Building_Energy_Optimization/links/592fce220f7e9beee761a995/Are-Genetic-Algorithms-really-the-best-choice-for-Building-Energy-Optimization.pdf
The following reading goes deeper into Genetic Algorithms:
- Genetic Algorithms
- Sastry, K., Goldberg, D. E., & Kendall, G. (2014). Genetic algorithms. In Search methodologies (pp. 93-117). Springer, Boston, MA. https://link.springer.com/chapter/10.1007/978-1-4614-6940-7_4
References
- Pardalos, P.M., Resende, M.G.C., (2002), Handbook of applied optimization. Oxford University Press.
- Baños, R., Manzano-Agugliaro, F., Montoya, FG., Gil, C, Alcayde, A., Gómez, J., (2011), Optimization methods applied to renewable and sustainable energy: a review. In: Renewable and Sustainable Energy Reviews, Vol. 15(4), pp. 1753–1766.
- Renner, G., Ekart, A., (2003) Genetic algorithms in computer aided design. In: Computer-Aided Design, Vol. 35, pp. 709–726
- M. Monks, B. Oh, J. Dorsey, Audioptimization: Goal based acoustic design, IEEE Computer Graphics and Applications 20 (3) (2000) 76–91.
- Turrin, M. (2013). Performance Assessment Strategies: A computational framework for conceptual design of large roofs. TU Delft.
- Elbeltagi, E., Hegazy, T., Grierson, D., (2005), Comparison Among Five Evolutionary-based Optimization Algorithms. In: Advanced Engineering Informatics, Elsevier, Vol. 19 (1), pp. 43-53.
- Guliashki, V., Toshev, H., Korsemov, C., (2009), Survey of Evolutionary Algorithms used in multi-objective optimization. In: Problems of Engineering Cybernetics and Robotics, Bulgarian Academy of Sciences, Vol. 60, pp. 42–54.
Computational Methods for Design and Research 7/7
Design Exploration Through Optimizationlink copied
This section is mostly extracted from Turrin (2013) pages 310-312 and reflects on the use of optimisation to explore design options in architectural design.
Optimisation techniques are commonly used to search a design space for solutions that meet specified performance goals (Monks et al., 2000). While finding an optimal or, in many cases, a sub-optimal solution to a design problem is valuable, optimisation can also be highly beneficial for exploring design options and gaining insights into the nature of the design problem.
Design exploration and searching for optimal solutions are different processes. In fact, optimisation is a converging process, whereas exploration requires also diverging steps in the process. Already in the 1990s researchers proposed different ways to make optimisation methods more diverging and thus more appropriate to support design exploration. These include for example evolving design objectives alongside the design variables, constructing more flexible design spaces, and defining criteria for ranking and selecting sub-optimal solutions.
Maher and Poon (1995) proposed a GA-based design system in which the objective function co-evolved with the design solution. Other academics developed interactive optimisation procedures whereby the user intervene in the process by modifying, adding or deleting variables, changing their variation domain, and introducing or removing constraints. Monks et al. (2000), used simulated annealing to assist in the preliminary design phase for acoustic measures, in which the user can optimize over materials and geometry either separately or simultaneously. Among the ones drawing attention on sub-optimal, Mourshed and Shikder (2011) point out that sub-optimal solutions are usually discarded and in most of the precedents they do not contribute to decision making after optimization runs. Mourshed and Shikder stress instead that ‘the discarded “inferior” solutions and their fitness contain useful information about underlying sensitivities of the system and can play an important role in creative decision making’. Based on this consideration, Mourshed and Shikder propose a visual method to analyse sub-optimal solutions. These are retained during optimization and represented in a fitness array visualization system.
In addition to this aspect, also a second point of value can be identified in sub-optimal solutions; and this is related to the specific nature of design. Following the description of the act of design given by Herbert Simon (1969), it is often counterproductive to focus on one ‘best’ solution, because the objective criteria that produce it are usually incomplete. Particularly in the area of form determination, many criteria are not easily expressed numerically. For certain aspects, the approach proposed by Luisa Caldas embraces this point of view and tries to overcome the issues of focussing on a single optimal solution. . Caldas and Norford (2002) developed a tool to optimsze the environmental performance of a building. This tool uses a GA as the search engine, a thermal and lighting simulation program to analyse the building performance and an AutoLisp routine for result visualisation. The authors explain that different optimisation runs may produce several design options with similar performances. As noted by the authors, this ‘may constitute valuable information to the designer, who is provided with several alternative solutions over which he can further overlap other design criteria not included in the optimization process’ (Caldas and Norford, 2002).
BGRID (Miles at al., 2001) is a decision support system for the conceptual design of commercial office-type buildings, which uses GAs to search for design options meeting several structural and architectural design requirements. The system allowed a designer to specify the layout of columns in the plan and define lighting and ventilation requirements. BGRID then retrieved a set of sub-optimal solutions, thus prompting further comparisons and analyses. The analysis of sub-optimal design solutions can highlight the need for introducing additional design criteria, or reformulating the search space through variable and constraint adjustments. More recently, several examples of optimization-based design exploration have been developed in early-stages of architectural design. Among the examples, Likai Wang (2022) proposed an exploration process using EvoMass, which is a building massing design generation and optimization tool in Grasshopper. Multi-disciplinary design
explorations have also developed rapidly. The review paper by Wang et al. (2024) provides a valuable overview.
Note: This educational material is intended for BSc students. During BSc studies, you are introduced to design exploration via optimisation. In more advanced studies, you will learn about more sophisticated methods for design exploration. If you wish to get a glimpse of these methods, check out the following publications:
- Pan, W., Sun, Y., Turrin, M., Louter, C., & Sariyildiz, S. (2020). Design exploration of quantitative performance and geometry typology for indoor arena based on self-organizing map and multi-layered perceptron neural network. Automation in Construction, 114, 103163.
- Danhaive, R., & Mueller, C. T. (2021). Design subspace learning: Structural design space exploration using performance-conditioned generative modeling. Automation in Construction, 127, 103664.
References
- Grierson, D.E., (1996), Conceptual design using emergent computing techniques. In: Grierson, D.E., Hajela, P., (Eds), Emergent Computing Methods in Design; Applications of genetic algorithms and neural networks, NATO ASI Series F, Computer and Systems Sciences, Vol. 149, Springer, pp. 150–161
- Maher, M.L., Poon, J., (1995), Co-evolution of the fitness function and design solution for design exploration. In: Proceedings of IEEE International Conference Evolutionary Computing, Perth, Australia, pp. 240-244
- M. Monks, B. Oh, J. Dorsey, Audioptimization: Goal based acoustic design, IEEE Computer Graphics and Applications 20 (3) (2000) 76–91.
- Mourshed, M., Shikder, S., & Price, A. D. (2011). Phi-array: A novel method for fitness visualization and decision making in evolutionary design optimization. Advanced Engineering Informatics, 25(4), 676-687.
- Simon, H.A., (1996) The Science of the Artificial, MIT Press, Cambridge, MA, USA
- Caldas, L., Norford L., (2002), A design optimization tool based on a genetic algorithm. In: Automation in Construction, Vol. 11, pp. 173-184.
- Caldas, L., (2006), GENE_ARCH: An evolution-based generative design system for sustainable architecture. In: Smith, I.F.C., (ed.), Lecture Notes in Artificial Intelligence, Springer-Verlag Berlin Heidelberg, pp. 109-118.
- Caldas, L., 2008. Generation of energy-efficient architecture solutions applying GENE_ARCH: An evolution-based generative design system. In: Advanced Engineering Informatics, Vol. 22 (1), pp. 59-70.
- Miles, J.C., Sisk, G., Moore, C.J, (2001), The conceptual design of commercial buildings using a genetic algorithm. In: Computers & Structures, Vol. 79, pp. 1583-1592
- Wang, L. (2022). Workflow for applying optimization-based design exploration to early-stage architectural design–Case study based on EvoMass. International Journal of Architectural Computing, 20(1), 41-60.
- Wang, Z., Akbarzadeh, M., & Aviv, D. (2024). Multi-objective design exploration for integrated structural-environmental performance of buildings: A review. Energy and Buildings, 114638.
Examples of Optimisation in the Early Design Stages (Relevant for BKB2WV3)
This section is mostly extracted from Turrin et al. (2011) and provides examples on the use of optimisation in architectural design.
As described in Turrin et al. (2011), looking at stochastic optimization processes for conceptual design in architecture, examples can be found in different fields since long time. One of the most traditional aspects is space layout planning, which was addressed based on stochastic optimization already in the late 90’s by Jo and Gero (1998); Park and Grierson (1999) use a multi-objective genetic algorithm in order to optimize the building layout with respect to the project cost and the flexibility of floor space usage; also hybrid techniques are used, such as in the case of the annealed neural network developed by Yeh (2006) by combining simulated annealing and neural network. Layout distribution on floors has been approached several times (Pham and Onder, 1992; Damski and Gero, 1997; Jo and Gero, 1998; Gero and Kazakov, 1998), as well as three dimensional space arrangement (O’Reilly and Ramachandran, 1998). Specifically applying optimization techniques to a performance simulation system, acoustic performance has been evolutionary addressed by Monks et al. (1998 and 2000). Focusing on energy, an exhaustive overview of optimization techniques applied to energy related aspects can be found in Baños et al. (2011). Differently, a more specific focus is given here to precedents using stochastic techniques combined with building performance simulations. These have been variously used. Specific aspects have been tackled through optimization, such as fenestration for daylight and energy performance (Caldas and Norford, 2002; Wright and Mourshed, 2009). Other approaches include broader aspects. Wang et al. (2005) use a multi-objective GA to evaluate design alternatives for both economic and environmental criteria. For thermal comfort and energy consumption, Magnier and Haghighat (2010) offer a recent example concerning design variables affecting the passive solar behaviour (such as size of the windows and thermal mass) and HVAC systems. By increasing the complexity of the optimization, attention is necessary for the time needed to compute the process. Magnier and Haghighat (2010) approach the challenge by diminishing the need of high numbers of GA generations. With this aim, the optimization is combined with a trained Artificial Neural Network. Focusing on similar design problems but on different optimization challenges, Diakaki et al. (2010) aim at supporting the designer in finding globally optimum solutions among alternatives and according to his/her preferences. The latter are considered by making use of weight coefficients to define the relative importance of design criteria. A compromise programming approach is used to optimize the design variables. Case studies are shown for criteria concerning energy consumption, investment cost and release of CO2 emissions; explorations are based on decision variables representing the selection of alternative materials for the building envelope and systems for space heating, cooling and hot water supply. Other examples can be found in Ooka and Komamura (2009), Mohamed et al. (2011), and others. A last note concerns interdisciplinarity. In the field of energy efficiency, an important contribution toward interdisciplinarity is recalled concerning Wright and Farmani (2001), which developed the simultaneous GA based optimization of building design fabric, HVAC system size and the supervisory control strategy. An integral design is proposed, which the author defines ‘whole building design’, aiming at overcoming the mono-disciplinarily or less integral nature of precedents research in optimization for thermal aspects. The topic of outdoor thermal comfort is also tackled through optimization techniques. A major precedent is illustrated in Chen et al. (2008), in which the authors aim at improving the outdoor thermal environment in summer by using GAs and a coupled simulation of convection, radiation, and conduction examined for variations in building and plant arrangements. Optimization for the design of semi-outdoor areas is not largely addressed, and precedents focus mainly on peculiar aspects of semi-indoor spaces. Such is the case of Jungfen et al. (2010), focusing on optimization of water spray systems for adiabatic cooling in the semi-outdoor spaces of the Shanghai Expo; Wang et al. (2010) draw attention to the importance of optimization of adiabatic cooling also for semi-outdoor areas, but do not actually show optimization methods. In the field of structural design, examples are numerous. Kaveh et al. (2008) use ant colony optimization and finite element in topology optimization to find the stiffest structure given a certain amount of material, in 2D and 3D structural models. Fanjoy and Crossley (2000) and Jakiela et al (2000) offer some of the many examples of use of GA based optimization for structural topology; Ishida and Sugiyama (1995) focus on columns, more commonly, other authors (Galante, 1996; Camp et al., 1998) focus on trusses and beams. Also hybrid methods are largely developed and applied. It is the case of a hybrid optimization algorithm based on the particle swarm and group search, developed by Shikai and Lijuan (2011) and used to investigate truss structures with continuous variables. Multidisciplinary optimisation has also been explored in the structural design field. Miles et al. (2001) proposed a GA-based method for structural optimisation that can integrate considerations about layout, lighting, energy consumption, and other building performance aspects.
Additional reading:
Curious to see more examples?
- Ekici, B., Cubukcuoglu, C., Turrin, M., & Sariyildiz, I. S. (2019). Performative computational architecture using swarm and evolutionary optimisation: A review. Building and environment, 147, 356-371.
References:
For the list of references, please consult the reference list of this article:
- Turrin, M., Von Buelow, P., & Stouffs, R. (2011). Design explorations of performance driven geometry in architectural design using parametric modeling and genetic algorithms. Advanced Engineering Informatics, 25(4), 656-675.
Examples Using Optimisation to Answer Research Questions (Relevant for BKB3WV4)
Examples MSc Graduation projects at ABE TU Delft:
- Evina Giouri (2017). Zero Energy Potential of a High Rise Office Building in a Mediterranean Climate. Mentors: Tenpierik M, Turrin M. For highrises, it investigates an integrated strategy by optimization for nearly zero energy. | Also published in: Giouri, E. D., Tenpierik, M., & Turrin, M. (2020). Zero energy potential of a high-rise office building in a Mediterranean climate: Using multi-objective optimization to understand the impact of design decisions towards zero-energy high-rise buildings. Energy and Buildings, 209, 109666.
- Stefanie Moumdjian (2020). Computational Design Analysis of Height Scenarios in Residential High-rise under BENG 2020. Mentors: Turrin, M., Bokel, R.M.J. It investigates whether the BENG regulations turn into a limitation to the target height despite the implementation of optimal design solutions.
- Andrea Fumagalli (2020). Energy Space Layout: Designing space layout with optimised energy performance. Mentors: Turrin, M; Tenpierik, M.J., Du, T. It explores and optimises the correlation between space layout and energy performance of a co-living residence in the Netherlands.
- Alessandro Passoni (2020). Computational method for football stadium renovation: A computational method for the renovation of football stadiums to facilitate designers into making decisions. Mentors: Turrin, M., Eigenraam, P. It explores how a computational method can be developed for stadium renovation to support the designer into making decisions in the early design phase, allowing them to explore multiple solutions that improve the initial performances of the stadium.
- Anna Tsagkalou (2020). Optimization for retrofitting educational buildings in Greece. Mentors: Turrin, M, Bokel, R. It investigates design options for energy efficiency in schools in Greece, by means of optimization.
- Despoina Pouniou (2019). Computational optimization for the facade design of a nearly zero-energy high-rise office building in the temperate climate. Mentors: Turrin, M; Tenpierik, M.J, ARUP. From computational optimization, it extracts guidelines for façade design of Zero-Energy highrise office buildings in temperate climate.
- Fatima El Hadji (2019). Passive-climate facades in high-rises in tropical countries based on computational optimization. Mentors: Prieto Hoces A, Jansen C, Turrin M. It investigates facade options to passively increase thermal comfort in tropical climates in high-rises based on optimization and data analytics.
Write your feedback.
Write your feedback on "Computational Methods for Design and Research"".
If you're providing a specific feedback to a part of the chapter, mention which part (text, image, or video) that you have specific feedback for."Thank your for your feedback.
Your feedback has been submitted successfully and is now awaiting review. We appreciate your input and will ensure it aligns with our guidelines before it’s published.
