Naive Bayes Classifiers (Two Classes)
-
Intro
-
Overview
-
Approaches
-
Conclusions
Information
| Primary software used | Jupyter Notebook |
| Course | Computational Intelligence for Integrated Design |
| Primary subject | AI & ML |
| Secondary subject | Machine Learning |
| Level | Intermediate |
| Last updated | November 19, 2024 |
| Keywords |
Responsible
| Teachers | |
| Faculty |
Naive Bayes Classifiers (Two Classes) 0/3
Naive Bayes Classifiers (Two Classes)
Naive Bayes classifiers are based on Bayes theorem and assumes each feature is independent given that the class is known. This tutorial reviews classification of data which contains two classes.
Steps followed to create a Naive Bayes classifier (binary) in this notebook:
- Create a dataset to be used
- Convert feature variable dataset to encoded labels
- Convert target variables to encoded labels
- Choose algorithm
- Train model
- Get Prediction
For this tutorial you need to have installed Python, Jupyter notebooks, and some common libraries including Scikit Learn. Please see the following tutorial for more information.
Exercise file
You can download the notebook version here:
Naive Bayes Classifiers (Two Classes) 1/3
Overviewlink copied
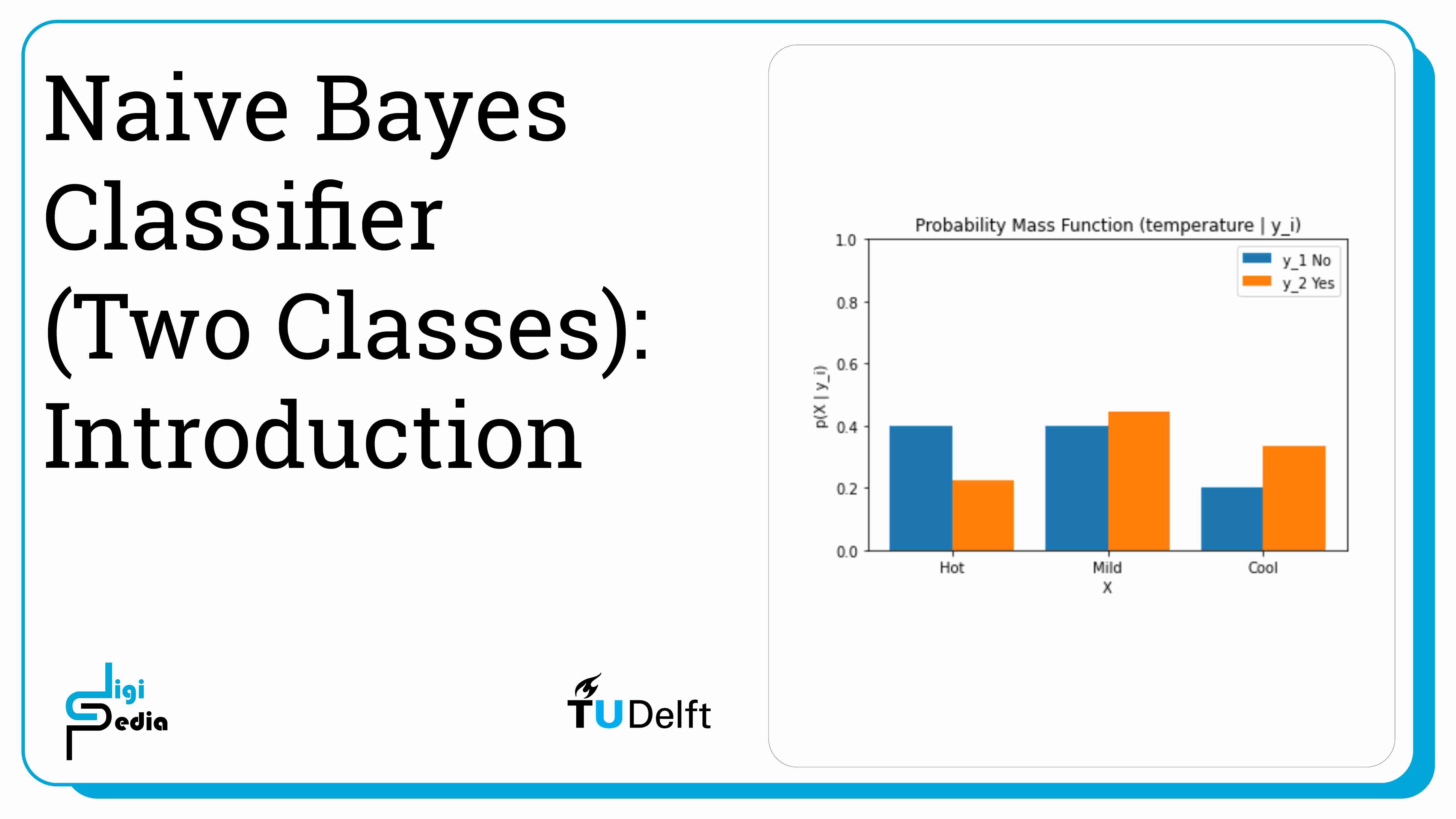
Bayes Theorem describes the probability of an event taking place considering prior knowledge about features that might impact the event. Naive Bayes classifiers are based on Bayes theorem and assumes each feature is independent given that the class is known. In other words, the classifier assumes that one feature being present in a class is not related to another feature being present in the same class. Features can be discrete or continuous. A discrete feature is discontinuous, only a select number of values are possible. Continuous features can be measured on a scale and can be divided into smaller levels. Discrete variables have a probability mass function. Continuous variables have a probability density function. The example in this tutorial works with discrete variables.
We want to predict if a football match will take place based on two features: weather and temperature. In this example, we will focus on two classes: yes (y1) and no (y2). The football match will either take place or not take place. The priors, or the probabilities of the match happening or not happening, must be known. These can be determined by dividing the number of times the class was assigned by the total number of datapoints. For the example below, the data is available for 14 past matches. Nine matches were classified as yes (y1) so the probability of the match taking place (P(y1)), is equal to 9/14. Five matches were classified as no (y2) so the probability of the match not taking place (P(y2)), is equal to 5/14.
Since, this example contains discrete variables, the likelihood represented by the probability mass function (p(X|yi) where i = 1, 2) must also be known. This describes the distribution of if a match went ahead in the past based on the weather and temperature conditions.
Bayes’ theorem states that the probability of the match taking place given a set of features of weather and temperature (p(X|y1)) is called the posterior. The posterior is equal to the likelihood, or the probability mass function (p(X|yi)), times the priors, or the probability of the match taking place (P(yi)), divided by the input data probability distribution.
If the probability of playing given the weather and temperature is lower than the probability of not playing given the weather and temperature, then the features are assigned to the no class. In other words, the prediction is to not play.
- If P(y1|X) < P(y2|X), assign sample X to y2 If the probability of playing given the weather and temperature is higher than the probability of not playing given the weather and temperature, then the features are assigned to the yes class. In other words, the prediction is to play.
- If P(y2|X) < P(y1|X), assign sample X to y1 If the probabilities of playing and not playing given the weather and temperature are equal, then the prediction can be assigned to either class.
- If P(y2|X) = P(y1|X), assign sample X to y1 or y2
Naive Bayes Classifiers (Two Classes) 2/3
Approacheslink copied
Approach 1: How to use Label Encoder
To graph the features and classes, they should be converted to a number. Use the LabelEncoder method to convert the labels into numbers. The LabelEncoder works separately for each feature so at the end, it is necessary to zip the features into a single list. Although it is possible to use the LabelEncoder for features, it is best practice to use the OrdinalEncoder which we will cover in Approach 2. More information is available in the SciKit Learn User Guide.
# Import LabelEncoder
from sklearn import preprocessing
# creating LabelEncoder
le = preprocessing.LabelEncoder()
# Converting string feature labels into numbers.
weather_encoded=le.fit_transform(weather)
temp_encoded=le.fit_transform(temp)
print("Weather:",weather_encoded)
print("Temp:",temp_encoded)
The output is:
Weather: [2 2 0 1 1 1 0 2 2 1 2 0 0 1]
Temp: [1 1 1 2 0 0 0 2 0 2 2 2 1 2]
The class labels also need to be encoded.
# Converting string class labels into numbers
label=le.fit_transform(play)
print("Play:",label)The output is:
Play: [0 0 1 1 1 0 1 0 1 1 1 1 1 0]
The LabelEncoder method encodes features individually, so they need to be combined afterward. This issue does not happen when the OrdinalEncoder method is used we will take a look at the Ordinal Encoder later in this notebook.
See the notebook for the output of this cell.
# Combining weather and temp into single list of tuples
features=list(zip(weather_encoded,temp_encoded))
print(features)
Next, train the model based on the dataset and then return the prediction based on a new value: overcast weather and mild temperatures.
# Import Categorical Naive Bayes model
from sklearn.naive_bayes import CategoricalNB
# Create a Categorical Classifier
model = CategoricalNB()
# Train the model using the training sets
model.fit (features,label)
# Predict Output
predicted= model.predict([[0,2]]) # 0:Overcast, 2:Mild
# Predict probability
predict_probability = model.predict_proba([[0,2]])
print("Predicted Value:", le.inverse_transform(predicted), " with ", predict_probability)
The output is:
Predicted Value: [‘Yes’] with [[0.13043478 0.86956522]]
TASK: Try changing the variables to predict if the match would take place if it was overcast and hot.
What about sunny and hot?
Approach 2: We should use Ordinal Encoder for features
When the dataset has more than one feature, it is best to first combine the features into a single list and then encode them using the OrdinalEncoder method. More information is available in the SciKit Learn User Guide.
# Get dataset with string features
training_set=list(zip(weather, temp))
print(training_set)
[('Sunny', 'Hot'), ('Sunny', 'Hot'), ('Overcast', 'Hot'), ('Rainy', 'Mild'), ('Rainy', 'Cool'), ('Rainy', 'Cool'), ('Overcast', 'Cool'), ('Sunny', 'Mild'), ('Sunny', 'Cool'), ('Rainy', 'Mild'), ('Sunny', 'Mild'), ('Overcast', 'Mild'), ('Overcast', 'Hot'), ('Rainy', 'Mild')]
# Create Ordinal Encoder
enc = preprocessing.OrdinalEncoder()
encoded_training_set = enc.fit_transform(training_set)
print(encoded_training_set)
The output is:
[[2. 1.]
[2. 1.]
[0. 1.]
[1. 2.]
[1. 0.]
[1. 0.]
[0. 0.]
[2. 2.]
[2. 0.]
[1. 2.]
[2. 2.]
[0. 2.]
[0. 1.]
[1. 2.]]
We can see that the trained model returns the same result.
# Train model again
model2 = CategoricalNB()
model2.fit(encoded_training_set, target_set)
# Predict Output
predicted2= model2.predict([[0,2]]) # 0:Overcast, 2:Mild
predict_probability2 = model.predict_proba([[0,2]])
print("Predicted Value:", le.inverse_transform(predicted2), " with ", predict_probability2)
The output is:
Predicted Value: [‘Yes’] with [[0.13043478 0.86956522]]
Naive Bayes Classifiers (Two Classes) 3/3
Conclusionslink copied
- Naive Bayes classifiers are based on Bayes theorem which assumes each feature is independent given that the class is known
- Discrete features are discontinuous, only a select number of values are possible. Continuous features can be measured on a scale and can be divided into smaller parts
- Naive Bayes classifiers require the following information to be known:
- The priors, or the probability of a class being assigned
- The likelihood, which is expressed by the probability mass function for discrete variables and the probability density function for continuous variables
- The posterior probability is equal to the likelihood times the priors divided by the prior probability of the predictor
- When a dataset has more than one feature, it is best to first combine the features into datapoints and then encode them using the OrdinalEncoder method. More information is available in the SciKit Learn User Guide
- After training a Naive Bayes Classifier, it can be used to predict the probability of a class being assigned given a new feature vector. In the example in this notebook, the classifier can predict the probability of a football match taking place given new weather and temperature data
Write your feedback.
Write your feedback on "Naive Bayes Classifiers (Two Classes)"".
If you're providing a specific feedback to a part of the chapter, mention which part (text, image, or video) that you have specific feedback for."Thank your for your feedback.
Your feedback has been submitted successfully and is now awaiting review. We appreciate your input and will ensure it aligns with our guidelines before it’s published.
